矩阵不可逆的条件
看完这节课,我就是感觉,如果有两个列向量共线,肯定就没有唯一0解,那么就会导致这个矩阵是不可逆: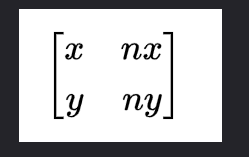
那列向量共线,是不是就是判断矩阵不可逆的唯一条件?(毕竟只要不共线肯定有解)
也就是说,如果我观察到一个方阵中有一个列向量共线,那么这个矩阵就一定不可逆,反之一定可逆。老师,这个结论对吗?
3808
收起
看完这节课,我就是感觉,如果有两个列向量共线,肯定就没有唯一0解,那么就会导致这个矩阵是不可逆: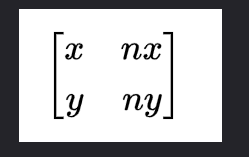
那列向量共线,是不是就是判断矩阵不可逆的唯一条件?(毕竟只要不共线肯定有解)
也就是说,如果我观察到一个方阵中有一个列向量共线,那么这个矩阵就一定不可逆,反之一定可逆。老师,这个结论对吗?