通过将矩阵化作行最简式求矩阵的逆,当对矩阵作过行交换后,得出的逆矩阵还是原矩阵的逆矩阵吗
波波老师,视频里的求解方法懂了,但是有个问题,就是"通过将矩阵化作行最简式求矩阵的逆,当对矩阵作过行交换后,得出的逆矩阵还是原矩阵的逆矩阵吗",希望回答一下哈:)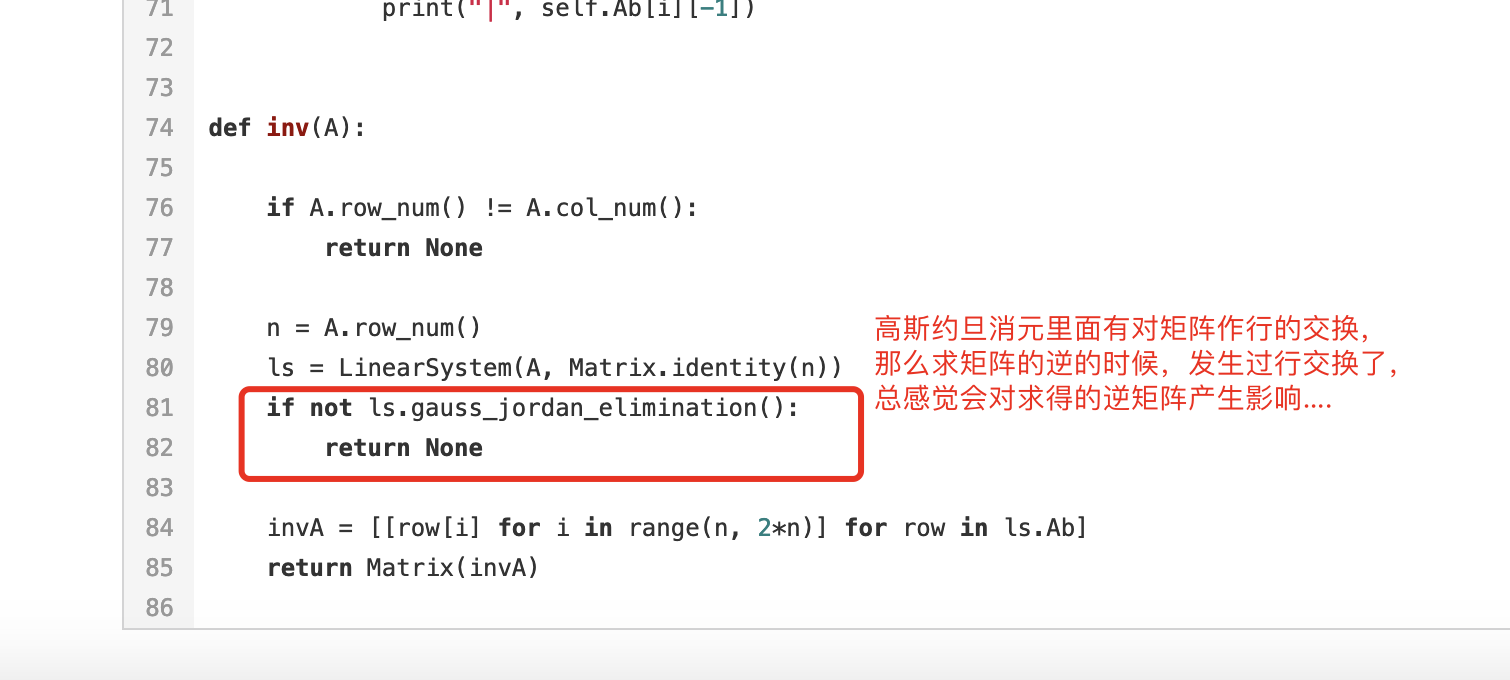
2509
收起
波波老师,视频里的求解方法懂了,但是有个问题,就是"通过将矩阵化作行最简式求矩阵的逆,当对矩阵作过行交换后,得出的逆矩阵还是原矩阵的逆矩阵吗",希望回答一下哈:)