把y=1的点都聚在一起，决策边界还是没有变化？

Question

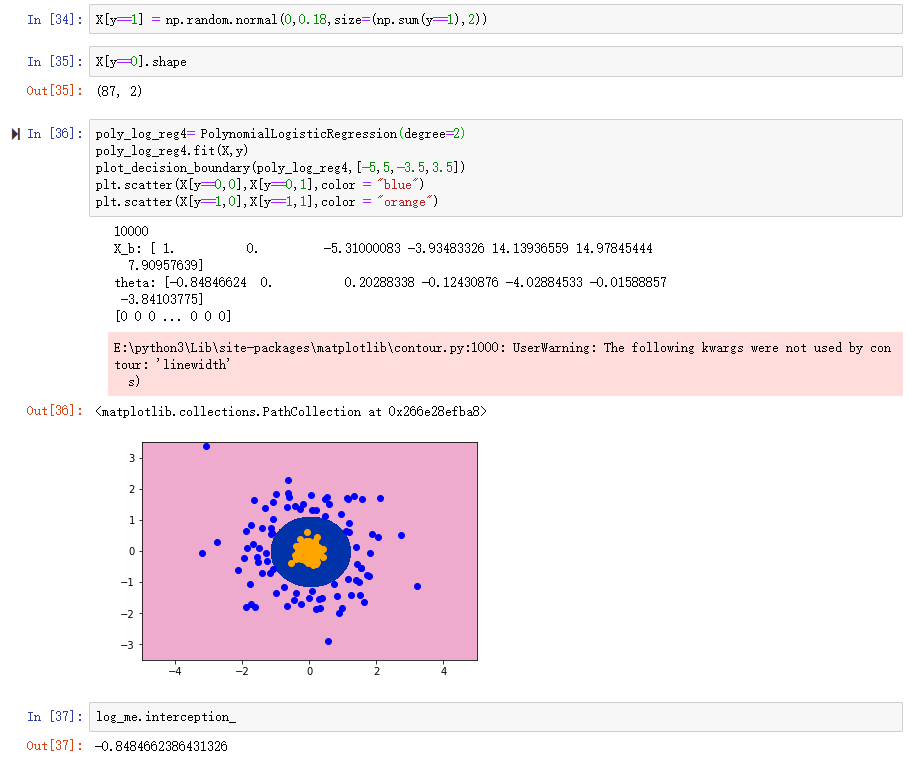
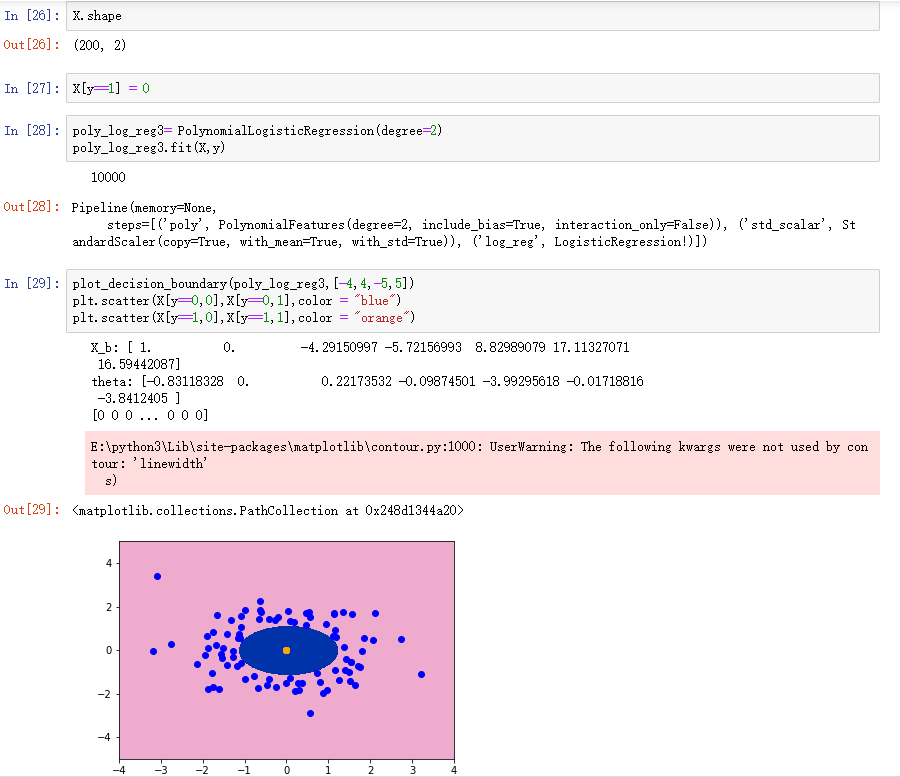
课上的demo我改了改，把决策边界内的点的x1,x2都缩小了，但是决策边界依然是那么大，贴着外圈。
我对于决策边界的理解就是预测值等于0.5的点的集合。图里面蓝色的点y等于0，对于梯度下降法的意义来说，每个蓝色点的出现都会使得决策边界向圆心靠拢，而每个黄色点都会使得决策边界向外扩张，而由于蓝色点的X1，X2相比较黄色点更大一些，根据梯度公式，下降的梯度（y_hat-y）*X,受到X大小的影响，蓝色点对于决策边界的影响力应该更大，决策边界应该被缩得很小才对。不过事实却打脸了。
而且极端情况下，所有y等于1的点都被我强制调整为0,0，这个决策边界还是那么大。。。

Answer 1

liuyubobobo 2019-04-18 17:32:00

大赞实践精神和对问题的思考！

首先，根据你绘制的第二张图，决策边界确实变化了：）

其次，你叙述的“每个蓝色点的出现都会使得决策边界向圆心靠拢，而每个黄色点都会使得决策边界向外扩张”不对。这是因为，逻辑回归的概率是有sigmoid函数决定的，结果不是这个样子。不信，你可以取一个你绘制的决策边界上的点，带进去计算一下，你会发现p是0.5的：）

但是，你的直观思考，确实是非常有道理的，而你的直观思考，恰恰是为什么有SVM的原因。SVM算法，本质就是认为，决策边界不应该贴着某些点这么近。理想情况下，应该在这二者中间：）所以，继续往下看，你会发现，SVM就在解决这个问题：）

继续加油！：）

• 提问者 慕桂英雄 #1

  为什么“每个蓝色点的出现都会使得决策边界向圆心靠拢，而每个黄色点都会使得决策边界向外扩张”不对没太明白，不过决策边界上的点确实应该就是p=0.5这我赞同

• liuyubobobo 回复 提问者 慕桂英雄 #2

  因为这个概率值不等于到这两部分的距离，而是被sigmoid函数转换的。和这个图上，你看到的距离不等价。