非零行的判断
老师我这样理解,对不对:
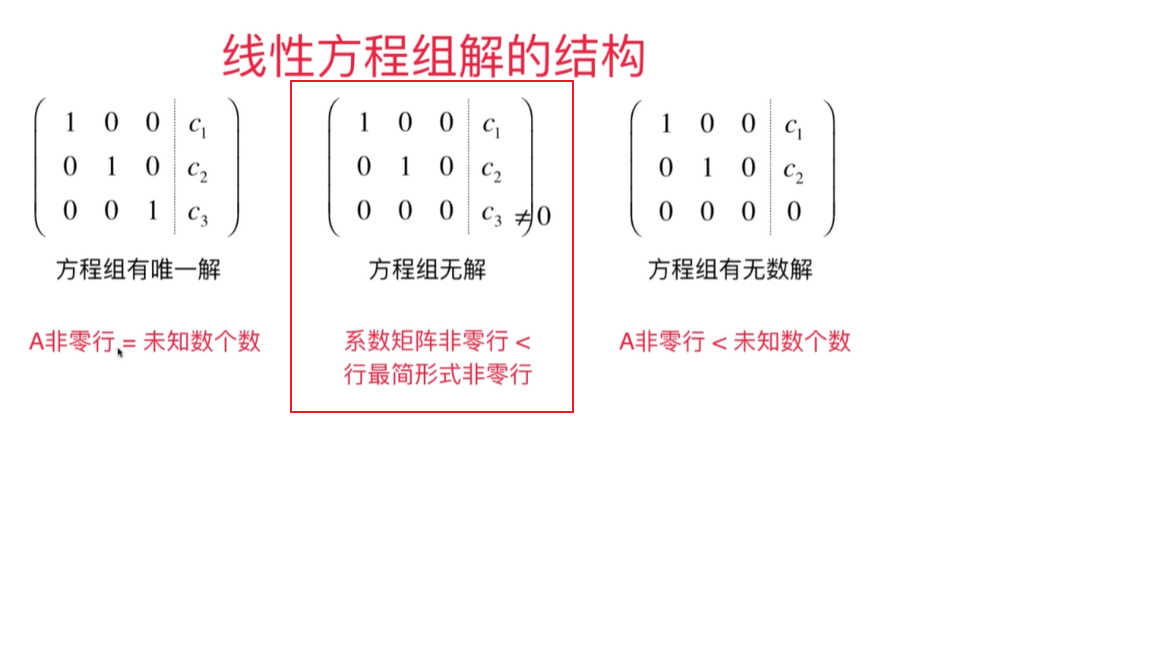
1 行最简形式的非零行,就是整个矩阵的非零行
2 未知数个数就是系数矩阵的列数
那对于,第二个矩阵来说,系数矩阵的非零行是2,行最简形式的非零行是3
未知数个数是3
那不是同时满足了,无解的条件和无数解的条件?
3485
收起

老师我这样理解,对不对:
1 行最简形式的非零行,就是整个矩阵的非零行
2 未知数个数就是系数矩阵的列数
那对于,第二个矩阵来说,系数矩阵的非零行是2,行最简形式的非零行是3
未知数个数是3
那不是同时满足了,无解的条件和无数解的条件?