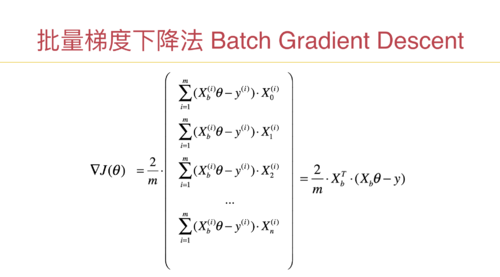
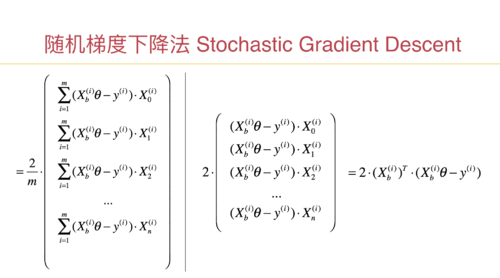
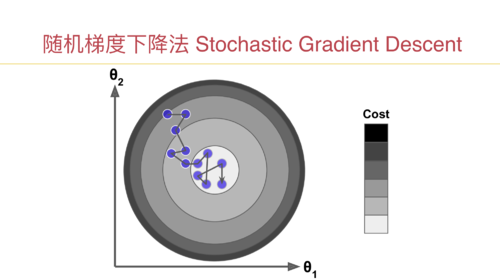
随机梯度下降法

Question

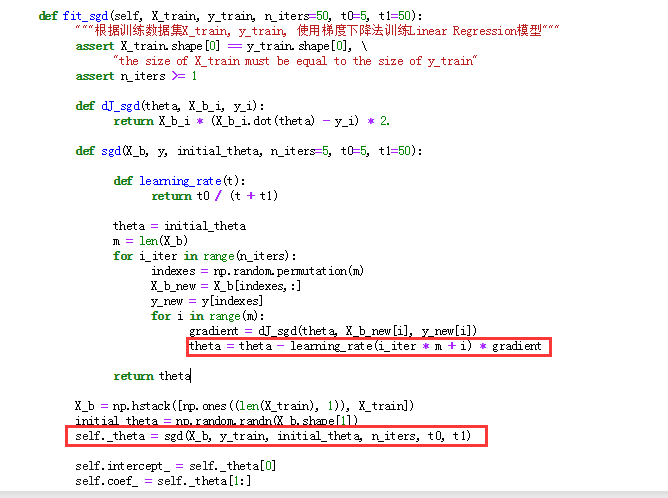
老师，这个逻辑理解的不是很透彻，第一个疑问是：随机梯度下降法涉及到多维特征的时候，我们每次都只取一行数据来计算，不太能在脑子里形成画面，这个时候就相当于在每个维度上取了一个特征点，然后多少个特征就相当于在多维空间中有多少个分布的特征点，由于采用了数据归一化，可以想象的到这些点特征值是在0~1之间，（1）这些特征点是一个线性的关系吗？（2）这些特征点所形成的损失函数图像是一个类似于二次幂函数的图像吗？因为之前我们的二次幂的损失函数图像（J）是一个特征多个样本的，还可以理解，但是现在这时候样本数据就选了一个，特征是有多个的，就有点理解不动了，思维也想象不到梯度的轨迹是怎么样的，不太理解ppt里面曲线的运动轨迹，这个随机梯度法能不能实现代码模拟绘图可以形象的看到。（3）不知道关于这个些疑问的学习方法和思考方向是不是对的，请老师指点一下，

第二个疑问是：随机梯度下降法运动轨迹有时候是正常的方向，有时候折回来了，（theta = theta - learning_rate(i_iter * m + i) * gradient ）是因为此时theta值小于learning_rate(i_iter * m + i) * gradient 导致theta值是负数的原因吗 就相当于是这时候遇到了局部最优解，前面出现了一个坡度，此时是从局部最优解往全局最优解移动的一个过程，所以走了回头路。

Answer 1

liuyubobobo 2019-06-19 06:23:13

我觉得可以这样理解这个问题：

首先，如果你能想明白梯度下降法的话，就是一个很好的开始。在梯度下降法中，我们每次寻找的梯度方向是这样计算出来：

注意，这个梯度向量，是n维的，每一个维度的计算，都用到了所有的m个样本的信息，因此每一维度的计算力，那个求和符号上，都有一个m。

现在，假想：

我们的样本数量只有一半，梯度怎么求？

其实，还是这个式子。只不过每一个求和符号取得这个m个样本，只有一半了；

我们的样本数量只有1/10，梯度怎么求？

还是这个式子。只不过每一个求和符号取得这个m个样本，只有1/10了；

我们的样本数量只有1个，梯度怎么求？

还是这个式子，只不过，m只剩下一个样本了。

这就是随机梯度下降法这个式子的由来，在下面的这页PPT中，左边是批量梯度下降法，右边是随机梯度下降法。右边就是左边的式子，但是m取1（相应的X只取一个样本）：）

当然了，这里m=1，不是致我们的样本只有一个。可以理解成，批量梯度下降法结合了所有的样本信息，获得了一个绝对正确的梯度；而随机梯度下降法，则只取一个样本，获得了一个梯度。这个梯度近乎一定是不准确的。这里所谓的准确，是指：是不是损失函数下降的最大方向。

所以，你的第二个疑问，折回来，就是因为通过这一个样本得到的梯度，和通过整体样本计算出的梯度，方向是相反的，不一样的。是错误的。

但是，这个梯度虽然不准确，甚至在有的时候，会向着正确梯度的反方向进行，但是，实践证明，这个梯度依然能够指导我们，一点一点找到一个极值位置。这背后的原因，涉及到的内容，超过这个课程的范畴了，可以参考这个问答：https://coding.imooc.com/learn/questiondetail/98263.html

你可以简单直观地理解成，参考了一个样本的信息，毕竟也是参考了信息的。虽然微不足道，但是经过在反复多轮以后，也帮助我们完成了任务：）

当然了，通过上面的分析，你就可以看到，批量梯度下降法，每次求梯度使用了全部样本，随机梯度下降法，每次求梯度使用了一个样本（优势是极大减少了运算量）；那能不能，每次使用部分样本（比一个多，比全部少）。

能。课程后续会提及，这就是小批量梯度下降法。也可以参考这个问答：https://coding.imooc.com/learn/questiondetail/42928.html

最后，这个课程PPT中给出的这个图，就是对于一组二维数据，应用随机梯度下降法绘制出来的图。只不过，由于这个课程没有这么详细的讲解绘图相关的编程，所以，我没有带领大家详细用代码汇出这个图而已：）

继续加油！：）

• 提问者 霸气的小羊 #1

  谢谢老师，我再消化消化

• 提问者 霸气的小羊 #2

  我重新整理了一下思路，
          一开始我理解成先随机取的一个样本通过这一个样本求得的损失函数（一个样本好像也不太能求切线什么的，然后把θ想象成了只有一个），我仔细又屡一遍，其实每次是在损失函数▽J(θ)里面随机设定的一个样本，可以想象成导数公式▽J(θ)是先求得的，只是在每次拿到样本i之后，换算出来的单个样本的导数，所以导致每次拿到的导数误差比较大，损失函数▽J(θ)和θ其实也都是铺满整个多维空间的，只不过和批量梯度下降法比起来精确度太差了，给人的感觉图像很稀疏，【theta = theta - learning_rate(i_iter * m + i) * gradient 】 ，其实从公式来分析，
          然后每次随机梯度下降的时候第n次单个样本数据求导后（这里单个样本的导数不准确的原因）得来的η值（learning_rate(i_iter * m + i) * gradient） 和前一次（n-1）的样本数据的theta之间的误差较大，而前一次的theta值又是更靠前的样本数据一步步计算逼近而得到的，是不是因为这部分误差导致的梯度轨迹像折线图一样。
         老师，我这样理解应该还是有错误的地方，不过感觉比之前的理解更深入了一些，请老师在简单指点下 。

• liuyubobobo 回复 提问者 霸气的小羊 #3

  我觉得基本没毛病了：）

点开查看后面1条评论