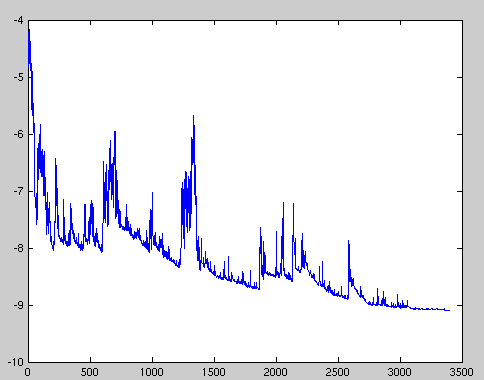
该怎么理解随机梯度必然会下降这个操作？

Question

for i in range(m):                    

    gradient = dJ_sgd(theta, X_b_new[i], y_new[i])                     

    theta = theta - learning_rate(cur_iter * m + i)

将样本地址随机后，对每一个样本做循环，求出随机梯度后，乘以不断减小的单位小量，对theta做减法，使theta不断向梯度的负方向（反方向）前进。

Answer 1

liuyubobobo 2018-05-19 16:48:01

首先，随机梯度下降法不是必然下降的。在课程中，我使用了以下图片：

仔细观察，在一些step中，我们的目标函数不是下降，而是上升的。如果查看stochastic gradient descent的wiki（https://en.wikipedia.org/wiki/Stochastic_gradient_descent），也会看到这样一幅图：

更可以清晰地看到，随机梯度下降法不是每次都下降的。（事实上，这个图是基于小批量梯度下降法做出的。小批量梯度下降法也可以理解成是梯度下降法的一种，在课程的后面会有所提及。）

但是，随机梯度下降法会高概率的向梯度下降的方向前进（但不一定是梯度下降最快的方向，注意这里和批量梯度下降法的区别），并且如果迭代次数足够多的话，整体趋势一定是逐步向下的。因为根据所有数据计算出的方向，一定是大部分数据所反映的方向。在我们随机选取数据的时候，虽然偶尔会选到一些数据，指向梯度上升的方向；但一定大部分数据，依然会指向梯度下降的方向（不然整体方向就不会是梯度下降的方向）。只要迭代次数足够，整体趋势是向梯度下降的方向前进的：）

• 提问者 用户Leon #1

  非常感谢！

• 提问者 用户Leon #2

  ”但一定大部分数据，依然会指向梯度下降的方向（不然整体方向就不会是梯度下降的方向）。“是不是因为-eta*gradient，所以才导致他指向梯度下降的方向。

• liuyubobobo 回复 提问者 用户Leon #3

  gradient的计算式借助数据的。在批量梯度下降法中，使用所有数据，而在随机梯度下降法中，只使用一个数据（相应的小批量梯度下降法中，使用一个数据的子集）。是的，整体-eta*gradient指向下降的方向。