梯度下降法和梯度上升法的收敛情况

Question

波波老师，我想问下，就是梯度下降法和梯度上升法，最终迭代后梯度是不是都会趋向于0？还是说两者的情况不一样。我自己就2维和3维上的感觉而言，迭代到最后找到的最小值（最大值），它在代价函数上的相应梯度都应该接近0才对。那本节课里面使用的梯度上升法，迭代到最后得到最大值结束的那几个几个梯度都是挺大的。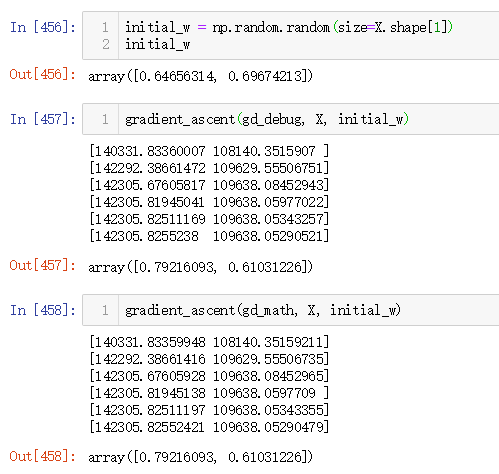

造成这样的情况是不是单位化w的原因？还是说，我本身对迭代到最后梯度应该趋向于0的理解有问题？

Answer 1

liuyubobobo 2018-11-19 17:22:10

非常好的问题！

梯度是否最终趋向于0，不是由算法决定的，而是有搜索的“曲面”是怎样的决定的。如果这个曲面有极小值，梯度下降法就一定会收敛到这里，之后梯度为0；同理，如果这个曲面有极大值，梯度上升法就会收敛到这里，最后梯度为0。（当然要有合适的参数。）

但是，如果曲面没有这个极值，梯度下降法或者梯度上升法肯定不会收敛。

很遗憾，我们要优化的PCA的函数本身，是没有极大值的。所以会遇到这种问题。（而我们之前所解决的线性回归问题，包括之后要用梯度下降法解决的逻辑回归问题，其最优化函数都是有极小值的，所以适合使用梯度法求解。）

我们的PCA优化问题，本质其实是一个带约束的求极值问题。这个约束就是，w的模要为1。回忆一下，这个结论是非常重要的，是得到我们PCA最终搜索的目标函数的一个重要的桥梁！所以，这个过程，w必须单位化！

对于带约束的求极值问题，使用梯度法并不是最好的求解策略。PCA本身其实具有非常好的数学解。但是由于在这个课程中，我不想牵扯到太多的数学概念，让大家学习机器学习的时候被吓跑，所以没有介绍PCA的数学解。（事实上，PCA的数学解极其综合，近乎能用到线性代数领域的所有主要知识，以及统计学中的很多概念。）

在这里，虽然梯度上升法不是最好的求解策略，但是对于大多数简单的数据，勉强能得到可以使用的解，所以，在这里，我们就使用这样的方式求解了。后续，我们会直接使用scikit-learn为我们提供的PCA接口，来处理更加复杂的数据。这个求解过程，以让同学们理解PCA的工作原理为主。对于PCA，希望同学们主要掌握，它到底是根据什么原则，把高维空间降低到了一个怎样的低维空间。原始高维空间和降维后的低维空间之间的关系。至于具体的计算求解方式，可以不作为重点：）

继续加油！：）

• 提问者 青影wz #1

  非常感谢！

• 提问者 青影wz #2

  老师，那这里用随机梯度下降法的话是不是就存在问题，最终得到的值和梯度下降不同，我实验了很长时间了，最终结果都是有问题的，还是我代码问题？