运用多项式核函数和直接使用多项式特征SVM结果差异
波波老师,我理解了核函数的思想:先不将x(i),x(j) 添加多项式特征转化为x’(i),x’(j), 再做乘法,而是直接对原来的两个样本进行数学运算,直接计算出x’(i),x’(j) 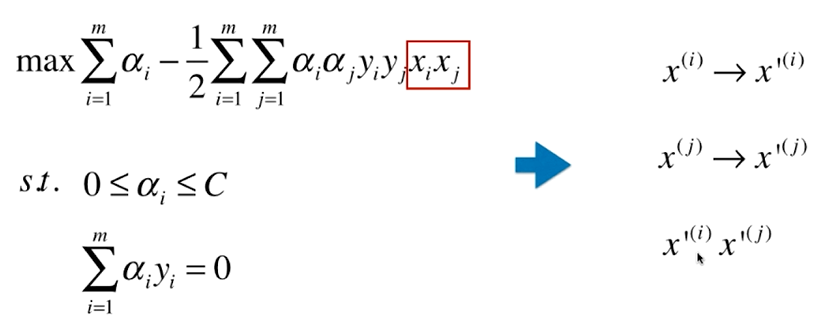 在这张图中,一直到这一步骤,多项式核函数和先多项式转换数据再SVM应该是一样的吧?您在视频中说应用核函数技巧,省去对原数据先进性变形,再对变形后的结果点乘的运算步骤,但是不使用核函数其实可以达到等价效果,那么为什么代码实现的时候,最终观察到的决策边界图案是有区别的呢 ?
在这张图中,一直到这一步骤,多项式核函数和先多项式转换数据再SVM应该是一样的吧?您在视频中说应用核函数技巧,省去对原数据先进性变形,再对变形后的结果点乘的运算步骤,但是不使用核函数其实可以达到等价效果,那么为什么代码实现的时候,最终观察到的决策边界图案是有区别的呢 ?
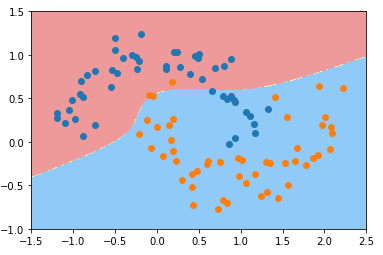
使用多项式核函数的决策边界
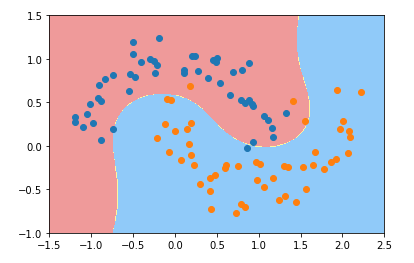
PolynomialFeatures预处理的决策边界
1656
收起









