关于标准化的几个问题

Question

看了7.3节、7.5节和本节的课程，以及问答区里的一些内容后，对标准化这一问题仍然吃得不是很透，存在几个方面的问题，还望老师或其他大牛帮忙解答 ：）

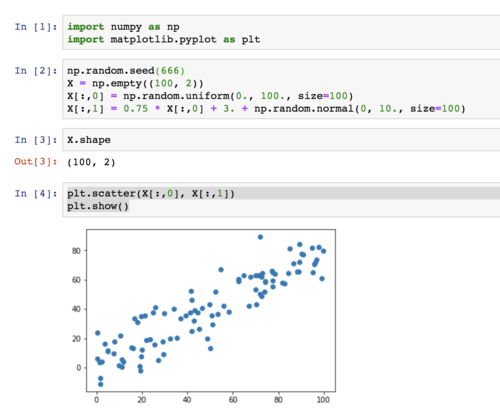
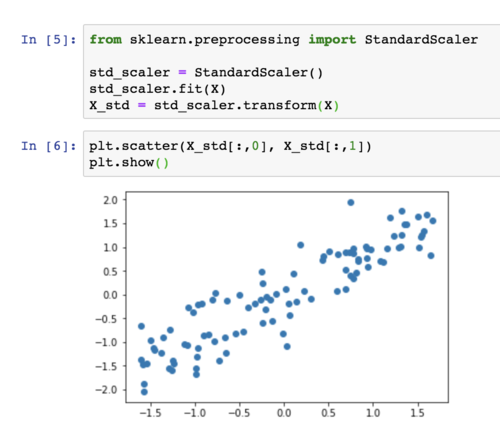
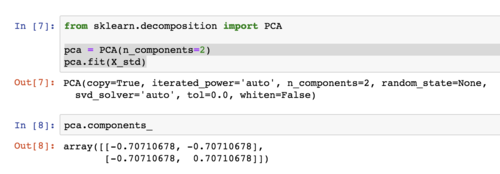
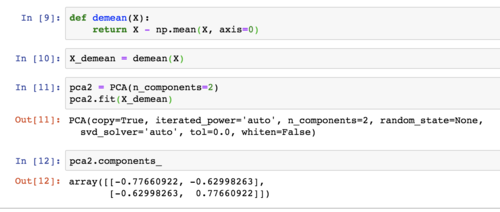
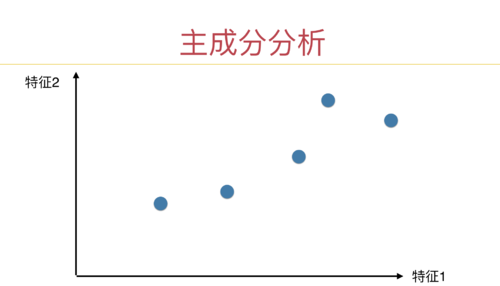
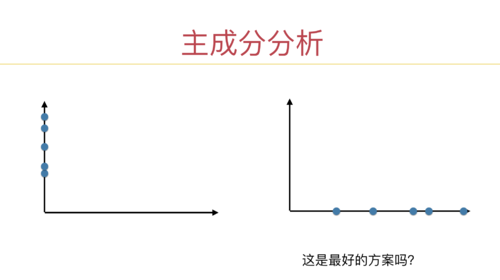
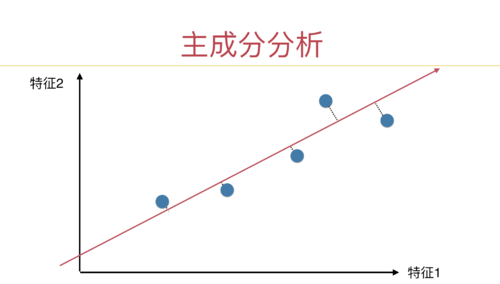
1、课程中说做PCA之前不用标准化，在问答区中有同学提出了不同意见；浏览了问答区的相关内容后，还是不明白为什么不能标准化。如果有三个样本，每个样本有两个维度，其中一个维度的样本数值分别为1、2、3，而另一个维度的样本数值分别为10000， 10100、10200，虽然后者方差更大，但前者更能体现数据之间的差异；不做标准化的PCA的结果使得主成分轴极度倾斜，降维后的数据基本上体现的是后一维度的内容，前一维度的信息很大程度上被丢弃了，这样是否合理？这一问题如何克服？如果说均值方差标准化使得数据变得非线性了而导致不能再进行PCA，那有没有什么其他的标准化方法可以替代它呢？

2、老师在https://coding.imooc.com/learn/questiondetail/98019.html中提到了主成分轴极度倾斜的问题，并提出在降维之后可以对低维数据做标准化处理。这里我不明白的是，做完PCA之后，进行knn判别之前，如果用均值方差标准化对数据进行处理，那每一个维度的方差都变成1了，而PCA的作用就是找到方差最大的几个主成分，那这样一来，做PCA的意义又何在呢？这和从原始数据里随便取出k个维度的数据，然后对每个维度做均值方差标准化有什么差别呢？最终得到的结果都是k个方差为1的序列不是吗？这就是我另外一个不太明白的地方

3、在实际生产工作中会发现，某些维度方差大，往往是因为噪音大（即这一维度容易受到随机无关因素的干扰），有些维度方差小，往往是因为噪音小（即这一维度不容易受到环境因素干扰），但PCA将后者这样相对稳定的维度的信息被丢弃了，使得PCA的结果往往是噪声的体现。因此，我们必须人为地去选择像后者这样的因素作为评判因素，从而使得PCA无用武之地，机器学习的应用效果大打折扣。这样的问题有没有什么办法克服呢？

谢谢

Answer 1

liuyubobobo 2019-04-30 07:17:03

1.

PCA不能做标准化，是因为，PCA要做的事情，就是最大化方差。把数据标准化以后，方差肯定为1，改变了原始数据的方差，也就谈不上找到主成分，来最大化方差了。

我让大部分提出这个问题的同学，都去实际试验一下，将数据标准化以后，会发生什么。但看来很少有同学会实验。我借你的问题，写一段代码，展示一下：

首先，我们生成随机数据。这里生成的随机数据，我们还是用和课程同样的数据生成方式。

之后，我们对这个数据做标准化处理，得到X_std：

数据分布绘制出来看起来差不多，但要注意数据的坐标轴，完全不一样。现在，X_std数据的均值为0，方差为1。

现在，我们队X_std做主成分分析，看看结果是怎样的。节省时间，我们直接使用sklearn提供的PCA类。

可以看到，最终得到的这个主成分是谁？两个坐标轴，其实就是(1，1)和(-1, 1)（进行了正规化，所以是0.707），也就是和xy的方向转了45度角。这显然是不正确的。因为，我们生成的数据，斜率是0.75！最终的结果，这个方向应该接近tan值为0.75！

你可以使用demean的结果再做一遍PCA，确认一下这个结果。

当然，由于数据噪音的存在，这个结果不是完全的0.75。如果在生成数据的时候，降噪音向去掉，就会得到纯粹的0.75。但是，做了标准化，依然是1。因为我们进行了标准化。

重复一遍：PCA要做的事情，就是最大化方差。把数据标准化以后，方差肯定为1，改变了原始数据的方差，也就谈不上找到主成分，来最大化方差了。

2.

PCA的意义是降维。正因为他不是从n个维度中抽k个维度，所以才能最大程度保留原始数据信息。

比如课程中举的例子：

如果把这个二维数据降成一维数据，怎么降？

如果只是抽这个数据的横坐标或者纵坐标，就是这样的结果：

但是，我们直观的看，这个数据，如果放在一维。这个一维的轴，在二维中，应该是倾斜的，是这样的：

找到这个倾斜的轴，他的方向是谁，是主成分的主要目的。主成分降维的结果，是将所有的点，映射到这个倾斜的轴上。我们说，在这个轴上，每个数据的分布，和原始这些数据在二维空间中的分布，很接近。

3.

实际上，如果你看后续的课程，会看到，PCA本身是有降噪的作用的。

但是如果你的原始数据本身包含很大的噪音，那当然效果不好。不要说PCA效果不好，任何算法效果都不好。因为你的数据本身就有问题嘛，包含大量无效信息嘛（噪音）。所谓的garbage in，garbage out。

你的图片本身是一团马赛克，当然分辨不出它是谁。（人脸识别）

你的音频本身就是一堆噪音，当然分辨不出它说话的内容。（语音识别）

怎么解决？虽然各个领域有一定的降噪算法，但其实都效果有限。根本上，还是要从获得的数据的源入手，想办法让数据尽量少有噪音，甚至没有噪音。你给我一团马赛克，让我做图片识别。怎么改进算法都没用的。这就是我经常说的，数据本身在机器学习领域，比大多数人想象的要重要得多。这也就是为什么，大家要拼命去获得高质量的数据：）

加油！：）

• 提问者 神羅ten徵 #1

  老师您好，通过课程的学习，我已经了解到在PCA之前不适合进行均值方差标准化，老师在上一个帖子中给我的答复也加深了我对这一点的认识。这一点我是没有疑问的。
  1）对于第一个问题，我实际的疑问在于，在进行数据判别的时候，与其想要获得方差（绝对差异）最大的维度，我们往往更愿意获得一些相对差异较大的数据（即我们想要1、2、3这样的差异的维度而不是10010、10020、10030这样的差异的维度），这样一来，我们选择维度的标准就与PCA降维的标准存在不同，但我们又想借助于PCA这样的手段进行计算机自动降维而不是手动去挑选，这样的问题怎么解决呢？有没有办法不重新进行底层编程就让PCA降维的标准是“更能体现相对差异而不是绝对差异”呢？
  2）对于第二个问题，我换一种表述方式吧：
  ①PCA降维后的k维数据，在knn判别之前进行均值方差标准化，得到的是k个均值为0，方差为1的特征；
  ②从原始数据中随便选k维数据，在knn判别之前进行均值方差标准化，得到的是k个均值为0，方差为1的特征。
  发现两种方法得到的都是k个均值为0，方差为1的特征！您在课程中强调的是：PCA要做的事情，就是最大化方差。但是降维之后、knn判别之前的这一标准化步骤，把得到的k维数据（不管是通过PCA降维得到的还是手动随意选取的）的方差强行抹平为1，那这样一来何以体现出“PCA能够最大化方差”的优势呢？这是另一个我不太理解的地方。
  在这里答复似乎不能贴代码？对上述问题2做了一些编码尝试，发现随便选k维数据进行建模判别的准确度，有时高于PCA，有时低于PCA，不知这能否说明问题？

• liuyubobobo 回复 提问者 神羅ten徵 #2

  对于1），抱歉，我没有理解你的意思。对于2）PCA做的事情是降维。对于PCA，不能进行归一，才能得到合理的将为结果。降维后得到的数据，是新的特征。对于knn，做的事情是分类或预测。对于训练数据，必须做归一，才能得到合理的分类或者预测结果。knn的过程，已经和PCA没有关系了。PCA的最大化方差，也是为了能够合理的降维，而不是为了给knn做铺垫。你用其他方式降维，得到的预测结果和用PCA降维得到的预测结果不一样，不能说明PCA有问题。实际上，除了PCA，还有很多降维方式。对于你的数据，什么样的将为方式更合适，本身是一种超参数。在这个问答最后，我提及了其他降维方式：http://coding.imooc.com/learn/questiondetail/36607.html 继续加油！：）

• 提问者 神羅ten徵 回复 liuyubobobo #3

  好的，谢谢老师。我自己再琢磨下吧 ：）