soft SVM理论部分的疑问

Question

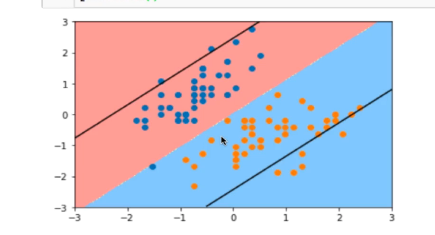
老师，按照优化函数来看，虽然对其他的样本有了一定的容错，但是那个min(|w|)并没有变吧？那么这样反推，支撑向量到决策边界的距离还是要最大才行，这样看着就感觉不对了，是不是因为加入了yita,所以就导致了min(|w|)这一块也变了？因为他已经不在那个w转置x+b=1的直线上面了，它所在的直线是 w转置x+b=1-η,我的感觉是之前的那个min（|w|）推导应该不成立了吧？就是当支撑向量在原来那条直线才可以推出这个min(1/2|w|²),而且观察图像也感觉在直线上的点，并不像完全在直线上，老师能解答一下这其中的变化吗？

Answer 1

liuyubobobo 2021-09-24 00:40:10

soft SVM 的最优化问题已经不是最小化 |w| 了，而是这个式子：上面的是最小化的内容，下面的是条件。是一个有条件的最优化问题，并且最优化式子的求解中添加了 eta。（注意，eta 不是已知量，而是未知量。）

对于这个最优化问题的求解，已经完全超过这个课程的内容了。实际上，这个最优化式子的求解，超过了大多数专业本科水平对数学的要求，甚至超过了大多数专业研究生水平对数学的要求（除非学习了凸优化的课程）。

如果对这后面的数学推导感兴趣，我在这里介绍了一些资料（或者在网上搜索的关键字）：https://coding.imooc.com/learn/questiondetail/gDANwYN0Zrg6K120.html

P.S. 刚才我搜索，这个问答里的第一个链接 down 掉了，我不确定是暂时的还是永久的，附一份网页快照的链接：https://webcache.googleusercontent.com/search?q=cache:sgbE3pqPx5wJ:https://shuzhanfan.github.io/2018/05/understanding-mathematics-behind-support-vector-machines/+&cd=15&hl=zh-CN&ct=clnk&gl=us

继续加油！：）

• 提问者 weixin_慕村8280326 #1

  老师，对于soft svm,支撑向量还满足| wx+b|=1吧？因为按照您之前hard svm的推导，如果min那一块优化函数不变，那从Hard svm到soft svm的变化只是让更多的数据进入到了两根定义决策边界的直线范围内，因为给了容错空间，所以相对的看wx+b=1那条直线，它就往外部走了一样，其实它的位置是没有动的，动的只是新给出的wx+b=1-n,所以理论上图上应该存在4条直线，老师我这样分析对吗？

• liuyubobobo 回复 提问者 weixin_慕村8280326 #2

  是的，满足 | wx+b|=1。但因为 w 和 b 都是我们要求的量，这个式子只是直线的一种表达方式而已，所以“其实它的位置是没有动的”这个描述是有问题的，条件变了，w 和 b 一动，整条线就动了。
  
  我不确定你说的 “4条直线” 是什么意思。但要注意，eta 是针对每一个数据点都有的一个对应的 eta，可以参考这里：https://coding.imooc.com/learn/questiondetail/4daeR64J02mYnWEp.html

• 提问者 weixin_慕村8280326 回复 liuyubobobo #3

  就是两条wx+b=±（1-n）
  两条wx+b=±1

点开查看后面4条评论