关于维度和决策边界的问题

Question

有几个关于SVM维度和决策边界的问题，不是很明白，有一点自己的理解，不知道对不对，还望老师帮忙解答和指正：）
1、之前在讲多项式特征逻辑回归时，是从决策边界及分类准确度的角度引入多项式特征的，即决策边界为曲线（面）时，使用线性方法没办法得到比较准确的决策边界（欠拟合），因此引入了多项式特征。是否可以换成从维度的角度理解呢？就是多项式逻辑回归也是一个将低维的数据投影到了高维后再进行分类的方法？
2、使用多项式SVM或高斯核SVM后，可以发现决策边界都是曲线（面），是否可以这样理解：将数据使用多项式SVM或高斯核SVM投影到高维之后，使用一个超平面对数据进行分类，而我们在二维平面上看到的决策边界实际上就是这个超平面切割得到的分类边界在二维平面上的投影？
3、对于多项式逻辑回归或者多项式SVM，我们在二维平面上看到的决策边界都会是相应的多项式曲线（如使用degree=2时，决策边界是二次曲线，使用degree=3时，决策边界是三次曲线）吗？
下图为使用PolyNomialFeatures（degree=2）+StandardScaler+LinearSVC步骤，对moons数据进行SVM分类后，得到的决策边界（横纵坐标范围已拓展），可以看出来决策边界像是二次方曲线（椭圆）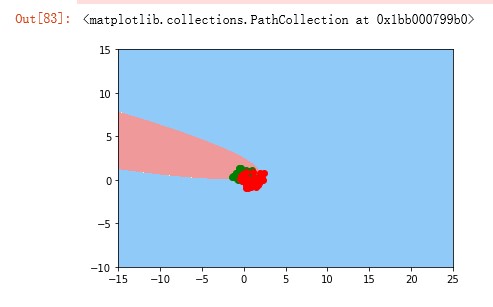

当使用多项式核（即StandardScaler+SVC(kernal='poly‘， degree=2)）时，二维平面上的决策边界看起来也像是二次曲线（双曲线）。那这两个图是否能支持我的上述观点呢（即：使用n次多项式特征，二维平面的决策边界就一定是n次多项式曲线）？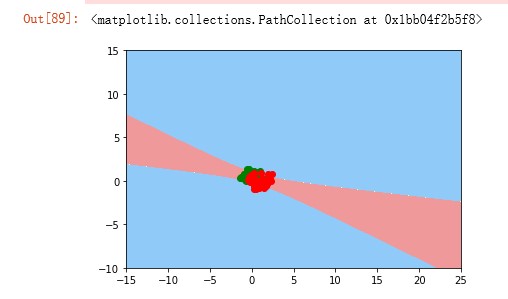
谢谢：）

Answer 1

liuyubobobo 2019-05-15 12:35:38

大赞！你的理解整体近乎都是正确的：）

1. 

多项式回归确实是一个降低为数据映射到高维的方法：）

2. 

我们在二维平面上看到的决策边界实际上就是这个超平面切割得到的分类边界在二维平面上的投影？这个说法我认为不够准确。关键在于什么是投影。

实际上，我们在这个课程中，之所以都是在二维平面上看到决策边界，是因为我们的数据是二维的。如果我们的数据是多维的，会给我们的可视化造成巨大的困难。对于3维以上的数据，则完全不可以直接可视化。所以，我在课程中，是以二维数据进行的举例，二维数据的决策边界，自然也在二维空间，而不是我们进行某种“投影”运算的结果：）

但是，我们可以想象，对于高维数据，SVM也将制作出一个或者多个“超曲面”分割整个高维空间，形成高维空间中的决策边界。

3.

如果经过PolyNomialFeatures后进行LinearSVM，或者SVM是多项式核，是的，决策边界就是多项式曲线。

但是，如果SVM是高斯核，则不是：）

继续加油！：）

• 提问者 神羅ten徵 #1

  理解了^_^
  想接着前面的问题再请教一个问题：在本课程中，之前的几种分类方法，都是从损失函数/目标函数的角度来引出分类算法的原理的，直到讲SVM时才提到了“线性可分”这一概念。那“线性可分”这一概念，在本课程已经提到过的几种分类算法中，只是SVM算法中才会用到，还是说前面的算法（如逻辑回归）也是用到了这个原理，也是将低维的线性不可分的数据映射到高维得到线性可分的数据后再进行分类？

• liuyubobobo 回复 提问者 神羅ten徵 #2

  之所以在SVM这里才提线性可分，是因为对于Hard Margin的Linear SVM，线性不可分意味着算法无法运行。但是当我们引入Soft Margin之后，就没有关系了。因为Soft Margin提供了容错机制，允许算法运行在线性不可分的数据上。而逻辑回归从根源上，就是可以应用在线性不可分的数据上，是可可容错的。对于逻辑回归，将数据映射到高维再做分类，只是有可能效果更好。（注意：只是有可能）多项式特征是一种特征工程的手段，而不是运行逻辑回归前必须做的事情：）

• 提问者 神羅ten徵 回复 liuyubobobo #3

  老师，对于您说的“映射到高维只是有可能效果更好”这一点我深有体会。比如说，对于两个属于不同类型的数据点，但是两者在各个特征上的数值都比较接近，因此，不管使用多项式方法，还是高斯核，因为没有引入新的有辨识度的特征，映射到高维这一工作只是将已有的辨识度不高的特征数据做各种数学运算而已（对于多项式，x接近，x的2次方或3次方也接近；对于高斯核，两者与其他各个地标的距离也都很接近），两个数据点在各个维度上的数值依然拉不开差距。这一问题的宏观体现就是：两个不同类型的数据集，在低维空间有部分重叠区域，这部分区域的数据点，即使映射到高维空间之后，在很大程度上依然是重叠的，导致映射到高维空间后，分类效果几乎没有明显改善。由于我这方面的经验不多，上述理解可能不准确。不知老师是否也有类似的体会，如果确实存在这样的问题，有没有什么好的解决办法？

点开查看后面2条评论