老师，对于主成分分析法，是为了求出该数据集在映射到哪一个方向上的方差是最大的。
对于这种方式可以用来降维，是因为它能够排除掉其他对于数据影响较小的特征，便于对数据进行分析
然而对于求其下一个主成分之前，要用其原始数据都减去前一个主成分，也就是将前一个主成分所对应的方向，从原始数据集中剔除了。
是不是可以理解为，求数据集的前n个主成分就是从数据集所留下来的“方向”中，不断地选取方差最大的那个方向。
如果是这样的话，对于多维空间而言，每个数据是不是都会有无数个方向，比如对于只有3个特征的数据集样本而言是不是可以求出其所对应的前4个，甚至前5个主成分？但它们之间的关系，并不是像二维空间那样两两垂直
如果是这样的话，对于多维空间而言，每个数据是不是都会有无数个方向，比如对于只有3个特征的数据集样本而言是不是可以求出其所对应的前4个，甚至前5个主成分？
这个结论是错误的。
==========
你说“对于这种方式可以用来降维，是因为它能够排除掉其他对于数据影响较小的特征”
PCA 没有排除掉特征。PCA 的过程不是每一次在现有的 n 个特征中选择一个特征扔掉。
这一点非常非常非常重要，近乎是理解 PCA 的核心。
以课程中的例子为例。
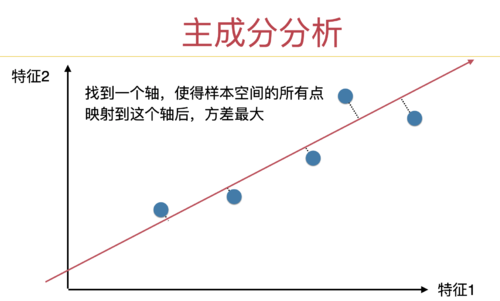
这样的一个两个特征的样本，做主成分分析以后，将二维降为 1 维，这个 1 维的方向是谁？既不是 x 轴，也不是 y 轴；所以我们既没有扔掉 x 轴，也没有扔掉 y 轴。这一个维度的方向，经过我们的计算，是一个“歪着”的轴。在这个轴上，即包含原有的 x 轴上的信息，也包含原有的 y 轴上的信息。
==========
我在这个课程的补充代码中，做了一个用三维特征数据做 PCA 降维的过程，可以参考这里：https://git.imooc.com/coding-169/coding-169/src/master/07-PCA-and-Gradient-Ascent/Optional-01-PCA-in-3d-Data/Optional-01-PCA-in-3d-Data.ipynb
请仔细观察，out[4] 是原始数据的点，把这样一个三维的数据降到二维，是 out[8] 的样子。注意，我们把三维降到二维，不是扔掉了 x 轴或者扔掉了 y 轴或者扔掉了 z 轴。所以，把三维降到二维的结果不是 xy 平面或者 yz 平面或者 xz 平面，而是一个在 xyz 空间里的平面，这个平面上既包含有 x 轴上的信息，也包含原有的 y 轴上的信息，也包含有 z 轴的信息。
进一步，将这个平面做降维，降到 1 维，得到的结果是 out[11] 的样子。依然是，这个一维的空间不是 x 轴或者 y 轴或者 z 轴，而是在这个三维空间里斜着的一条直线。
=========
所以，PCA 的过程，形象地理解是这样的：
对于一个三维数据，他肯定在三维空间，我们首先在这个三维空间里，寻找一个面（一个二维空间），注意，这个面不是简单地扔掉一个轴，在三维空间中有无数个面（而不是只有三个面），我们寻找的是那个能承载信息最多的面（保留方差尽量大）。
如果我们需要，还要降维，我们可以在这个面上找一条线，依然是，这个面上有无数条线（而不是只有两条线），但我们寻找的是哪个能承载信息最多的线。
==========
更抽象地看，对于一个 n 维数据，PCA 的过程，首先在这个 n 维空间找到一个 n - 1 维的子空间，这个子空间不是简单地扔掉这 n 维空间中 n 个轴里的一个。在 n 维空间里，有无数个 n - 1 维子空间，我们要求出那个承载的信息最多的 n - 1 维子空间。
如果要进一步降维，我们要在这个 n - 1 维的子空间中，去找一个 n - 2 维的子空间。n - 1 维的子空间中有无数个 n - 2 维的子空间，我们要求出那个承载的信息最多的 n - 2 维子空间。
以此类推。
=========
所以，对于一个 n 维空间来说，最多降到 0 维，此时就是一个点，但此时已经没有意义了，因为此时，所有的数据都聚到了这个点上，所有的信息都已经消失了。但理论上是可以的。也就是一个 n 维空间，只能找到 n 个主成分。在一个 n 维空间中，找不到第 n + 1，n + 2，n + 3 个主成分。
也就是我们在 3 维空间中，找不到一个 6 维的子空间。
继续加油！：）
登录后可查看更多问答，登录/注册
