样本数量与模型偏差和方差的关系

Question

老师您好。通过8.5-8.7的学习，了解了模型的偏差、方差和模型复杂度的关系，认识到模型的复杂度（如degree的大小）是决定一个模型是欠拟合还是过拟合的重要因素。在“学习曲线”一节中，通过观察当模型的误差趋于稳定后，训练曲线与测试曲线的绝对大小和相对高低，来判断模型是过拟合还是欠拟合。由于还没涉及到集成学习的问题，这里每次训练都是用的训练数据集中的全部或绝大部分样本，因此第8章只关注了模型复杂度（如多项式拟合中的degree、knn算法中的n_neighbors以及后面决策树模型中的max_depth等参数）与方差或偏差的关系，没有关注每次抽取的样本量与方差或偏差的关系。
在后面有关bagging算法的学习时，了解到每个基模型（如BaggingClassifier中的一棵决策树）所选取的样本数量是一个超参数，可以人为设置，为了获取最优的超参数，就得研究每个基模型训练样本数量对偏差及方差的影响。当然可以使用网格搜索的方式选取最优超参数，但这样太费时且有时会受到随机因素的影响，因此想先从理论上分析一下每次抽取的样本数量（如BaggingClassifier中的max_samples参数）与模型泛化能力的关系。由于我数学基础不太好，所以尝试感性分析了一下，但在分析过程中陷入了死循环，所以还想请老师帮忙看一看：
1）若每次抽取的样本数较少，则样本很可能无法反映总体分布的规律，导致偏差高，同时，每个样本单次被抽中的概率小，即每次抽取时样本差异大，导致不同的基模型得到的拟合/分类模型差异较大，导致方差高；当增加每次抽取的样本数量时，样本反映总体分布的能力增强，偏差减小，并且每次抽取的样本重复率增大，不同基模型得到的拟合/分类模型差别变小，方差减小。这样看来，在n_estimators固定的前提下，单次抽取的样本数量越多，偏差、方差均越小，模型泛化能力越强？
2）但事实好像又不是这样，若每次选取的样本数增加，那么outlier被选中的概率增加，导致每个基模型受到outlier影响程度也会增加，这样反而是影响模型的泛化能力的。
我用make_moons数据做了以下实验（n=1000，noise=0.3，test_size=0.2，使用的是BaggingClassfier算法，单棵决策树的超参数使用默认参数）,似乎证实了2）中的说法：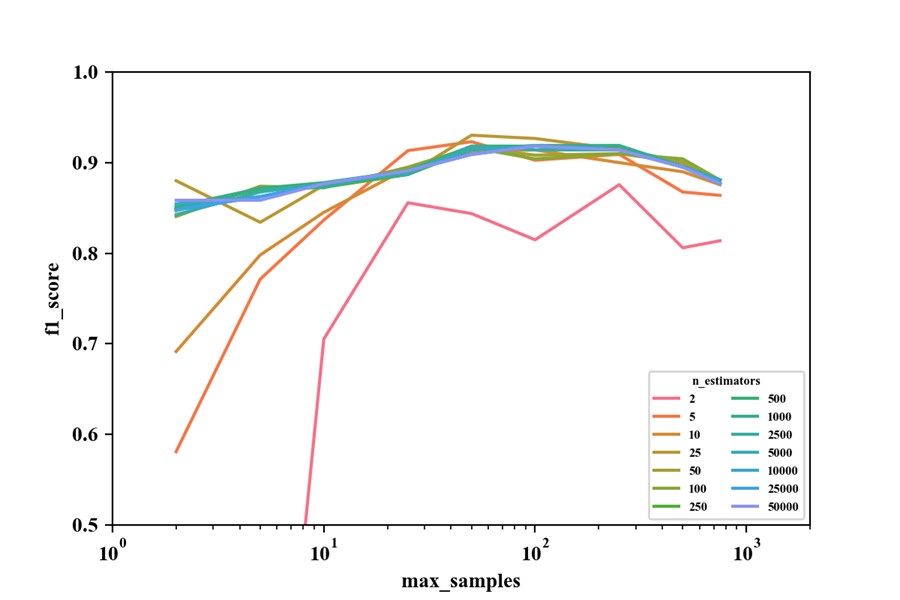


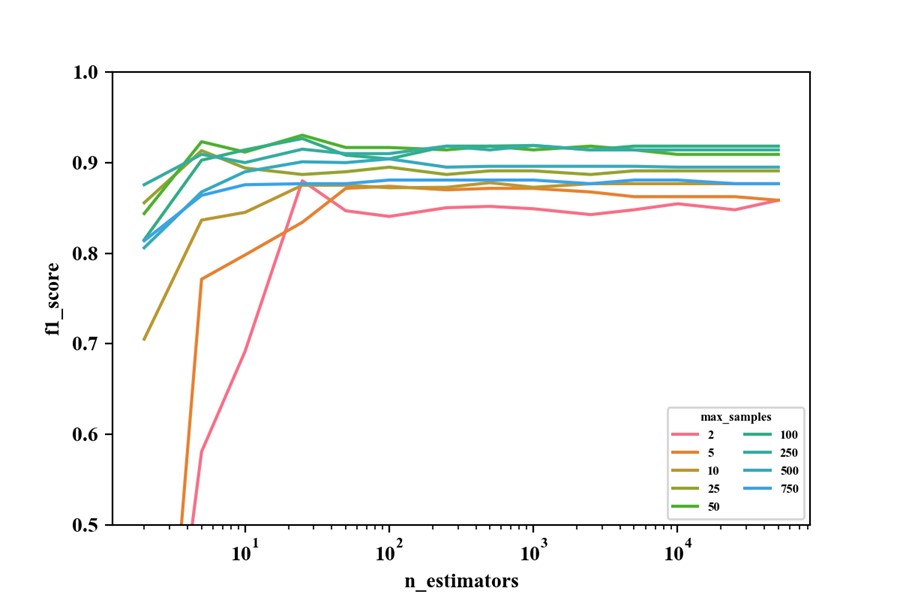
第一幅图中，n_estimators一定时，f1_score会随着max_samples的增加呈现出先上升后下降的趋势；第二幅图中，max_samples取较大值时，不管n_estimators取多少，其f1_score始终都不是最高的。

这样一来，max_samples不是越大越好实锤了吧？

但通过1）中的分析发现max_samples越大，方差、偏差均越小，泛化能力确实更好呀，这是矛盾了？

那么，是因为我在1）中的分析错了，还是除了方差和偏差之外，有第三个可以评价模型泛化能力的指标呢？

谢谢！：）

Answer 1

liuyubobobo 2019-05-22 02:58:37

赞一下实践精神！

1.

首先，说结论。对于随机森林来说，公认的最佳参数选取，是每一棵树的sample树都是n（即最大值），但是，采用放回取样的方式。所以，每棵树的数据终会有重复样本。实际采集到的不同样本数是小于n的（大概是2/3左右）。这个证明太复杂了，老实讲，也超出我的能力范围了。

而n_estimators，是越多越好，但是，数量多到一定程度，也就趋于稳定了。你的第一个实验的图示证明了这一点：）

更更关键的是，影响随机森林算法泛化能力的参数，远不止这两个。可以参考scikit-learn的文档。所有前缀是max_***或者min_***的参数，都是有意义的。https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html

2.

你的叙述中，提到了outlier，在这里，有必要说一下。如果你知道你的数据中有outlier，应该在数据预处理阶段剔除，而不是想办法让算法能够在有outlier的情况下还能有良好的表现。送给算法的数据，应该是肯定没有outlier的数据。虽然我们在这个课程介绍一些算法的时候，会看到有些算法的底层设计似乎在考虑outlier的影响，但近乎一定的，所有的算法都会在没有outlier的数据上得到更好的表现。这就是我一直强调的：在机器学习的世界中，数据很重要很重要很重要，可能比大多数同学想象得都重要。很多问题的关键可能不是算法，二是数据。这也是为什么，很多“搞机器学习”的同学，每天的工作其实是在做数据清洗。因为数据清洗真的能提高机器学习算法的水平。这也是为什么，特征工程很重要很重要，可以参考这里：http://coding.imooc.com/learn/questiondetail/40722.html

3.

最后谈一下泛化能力。泛化能力是我们训练模型的核心目的，因为，我们就是想要训练模型处理位置，但与此同时，泛化能力又是一个很虚的指标。为什么？因为我们不知道未知，怎么测试我们的模型在未知上的表现？

这也就是机器学习有的时候被称为“炼丹术”的原因。很多时候，我们在实验室中的一个次优模型，却能在生产环境下得到最好的结果。这也就是为什么，很多时候，我们分析我们的算法性能的时候，要看“趋势”，而不是一两个具体的值。真正的最优解，是在一个光谱范围里的。在一定的光谱范围中，我们很难说某一个值一定是最好的。因为，除了这些参数，数据质量，数据的代表性，等等算法无关的因素，也在影响最终算法的好坏。又说回了上面的问题：在机器学习的世界中，数据很重要很重要很重要，可能比大多数同学想象得都重要。

所以，你说f1_score不是最高的，这并不是什么问题。关键是稳定。因为最高不代表最好。我们要的是能够真实反映数据内涵的模型，而不是一个能测试出的最好结果的模型。实践表明，在大多数时候，实验室中找到的那个“能测试出的最好结果的模型”都不是泛化能力最强的模型：）

举一个例子，两个模型A和B，A得到的准确率是94%，B得到的准确率是95%。在机器学习的世界中，95%不一定是最好的。因为这个95%，可能只是因为你的测试数据的原因，恰好更高一些。但是，94%这个数字可以更好地反映出，你是用这个方法，基于这个数据，可以获得的模型的真实能力。换句话说，我可能有更高的信心，对于这个模型，在面对未知的时候，也能达到94%这么高。这是至关重要的。这就是我说的稳定的意思。

4.

至于评价模型泛化能力的指标，任何评价模型能力的指标都可以。关键是要基于未知数据，而不是什么指标。不同的指标都会或多或少的反映模型的一个侧面。这也是为什么机器学习中包含这么多不同的指标的原因。scikit-learn中封装的就有这么多（在metrics模块下）：https://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics 

关于和指标相关的更多讨论，可以参考这里：http://coding.imooc.com/learn/questiondetail/42693.html

再赞一下实践精神！

继续加油！：）

• 提问者 神羅ten徵 #1

  谢谢老师如此详细的解答！！
  
  除noise=0.35外，我又分别取了noise=0.15和noise=0.5，发现当noise越小时，确实如老师所说max_samples越大效果越好；而noise较大时，max_samples大到一定程度后，效果反而变差了，这并不是由于算法造成的，而是由于数据质量造成的。并且noise越大，这个现象越明显。
  
  这给我一个启示：当数据经过特征提取后，噪音仍然较大时，得谨慎考虑max_samples超参数的大小，若考虑不当，即使增大基分类器的个数，仍然不能使分类效果达到最优。
  
  再次谢谢老师！

• liuyubobobo 回复 提问者 神羅ten徵 #2

  大赞实验精神！：）继续加油！：）