分割整数的实例与代码

Question

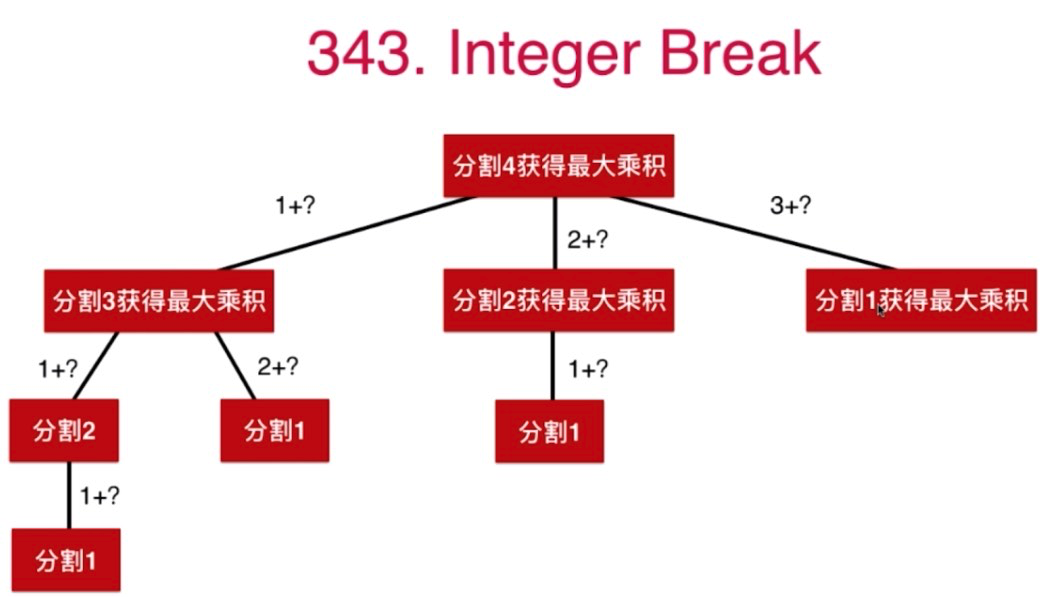
你好，老师！我反复听这个例子，都没能理解这个递推关系。可以在这里套入视频中以4的作为例子再解释一下？
在老师代码 memo[i]= max3(memo[i], j * (i - j), j * memo[i - j]); 中的j * (i - j)和j * memo[i - j]分别在图中实例代表哪些数的乘积？尤其为什么j * memo[i - j]可以作为备选项？

class Solution {
private:
    int max3(int a, int b, int c) {
        return max(a, max(b, c));
    }
public:
    int integerBreak(int n) {
        assert(n >= 2);

        // memo[i]表示将数字i分割(至少分割两部分)后得到的最大乘积
        vector<int> memo(n + 1, -1);

        // 自底向上：所以最小分成1， 1的最大乘积是1，所以1
        memo[1] = 1;
        for (int i = 2; i <= n; i++)
            // 求解memo[i]
            for (int j = 1; j <= i - 1; j++)
                // j + (i-j)
                memo[i]= max3(memo[i], j * (i - j), j * memo[i - j]);
        return memo[n];
    }
};

int main() {
    return 0;
}

谢谢！！！

Answer 1

liuyubobobo 2018-12-31 23:30:06

理解算法的关键，就是理解算法中的每一个变量，每一个函数的语义。

在这个程序中，memo[x]的语义是：将x分割几个整数的和，他们乘积的最大值。

在这个语义的基础上，对于任意一个数字i，我们将其进行分割：

或者将其拆成两部分，一部分是j的话，另一部分就是i - j，对应j * (i - j)；

或者将其拆分成三个或者三个以上的部分，此时，我们先考虑分割出的一个数字为j，之后，还要对剩下的i-j进行分割。剩下的i - j进行分割后乘积的最大值是memo[i - j]（回顾上面memo的语义！），在加上我们已经分割出的j，所以分割i得到的乘积的最大值，就是 j * memo[i - j]。

看看能否理解？继续加油！新年快乐！：）

• 提问者 慕标6347362 #1

  谢谢老师，新年快乐！具体到4这个例子，是不是这样理解？
  1."将其拆分成三个或者三个以上的部分，此时，我们先考虑分割出的一个数字为j，之后，还要对剩下的i-j进行分割。剩下的i - j进行分割后乘积的最大值是memo[i - j]" ：
  对应例子：4 = 1 + 1 + 2 -> 1 * （1 * 2）；
  2. "将其拆成两部分，一部分是j的话，另一部分就是i - j，对应j * (i - j)"：
  对应例子中的分割情况：4 = 2 + 2 -> 2 * 2 或者4 = 1 + 3 -> 1 * 3 ；
  
  谢谢！！

• liuyubobobo 回复 提问者 慕标6347362 #2

  对！将4拆分成多部分要注意，其实我们是将4拆分成：4 = 1 + (将3拆分)；4 = 2 + (将2拆分)；4 = 3 + (将1拆分)。括号里的内容就是所谓的子问题！也是memo[i - j]对应的内容：）

• 提问者 慕标6347362 #3

  非常感谢！