关于Bellman-Ford中第一轮松弛操作后dis[]数组的理解问题
老师，您好。我使用的就是您的“g.txt”这个图的对象。
我的算法代码如下，加了一些提示性的输出结果。我打印出了第一次对所有边松弛后的结果，打印出的dis数组是 [0 3 2 6 7].
但是我们之前假设dis[v]是从源点s到v的经历变数不超过k的最短距离。我不知道此时该如何理解在第一次对所有边松弛后中所得的结果 dis[3] = 6 ？这里的dis[3] = 6 是根据顶点1 （dis[1] = 4）所更新得到, 即对1-3这条边进行松弛操作得到。
还有对所有边进行一次松弛操作，则求出了到所有点，经过边数为1的最短路。在这句描述中，是指从哪个点出发经过边数为1的最短路？这里的“哪个点”应该是遍历图中的所有点吧？ 每次都在变化吗？
不好意思，我的问题有点长，请见谅。感谢！
正在回答
3回答
我有点儿忘记课程中有没有提及这个问题了。整体说，Bellman-Ford算法第k轮松弛操作，计算出的是从src到任一顶点经过k步的最小路径。这个说法基于我们的实现不严格。严格来说，计算的是从src到任一顶点，最少经过k步的最小路径。关键字是“最小”。
也就是基于我们的实现，我们有可能在第k轮松弛操作，求出经过大于k步的最小路径。但是，不一定在第一轮就能求出所有的最短路径。这依赖于我们遍历边的顺序。
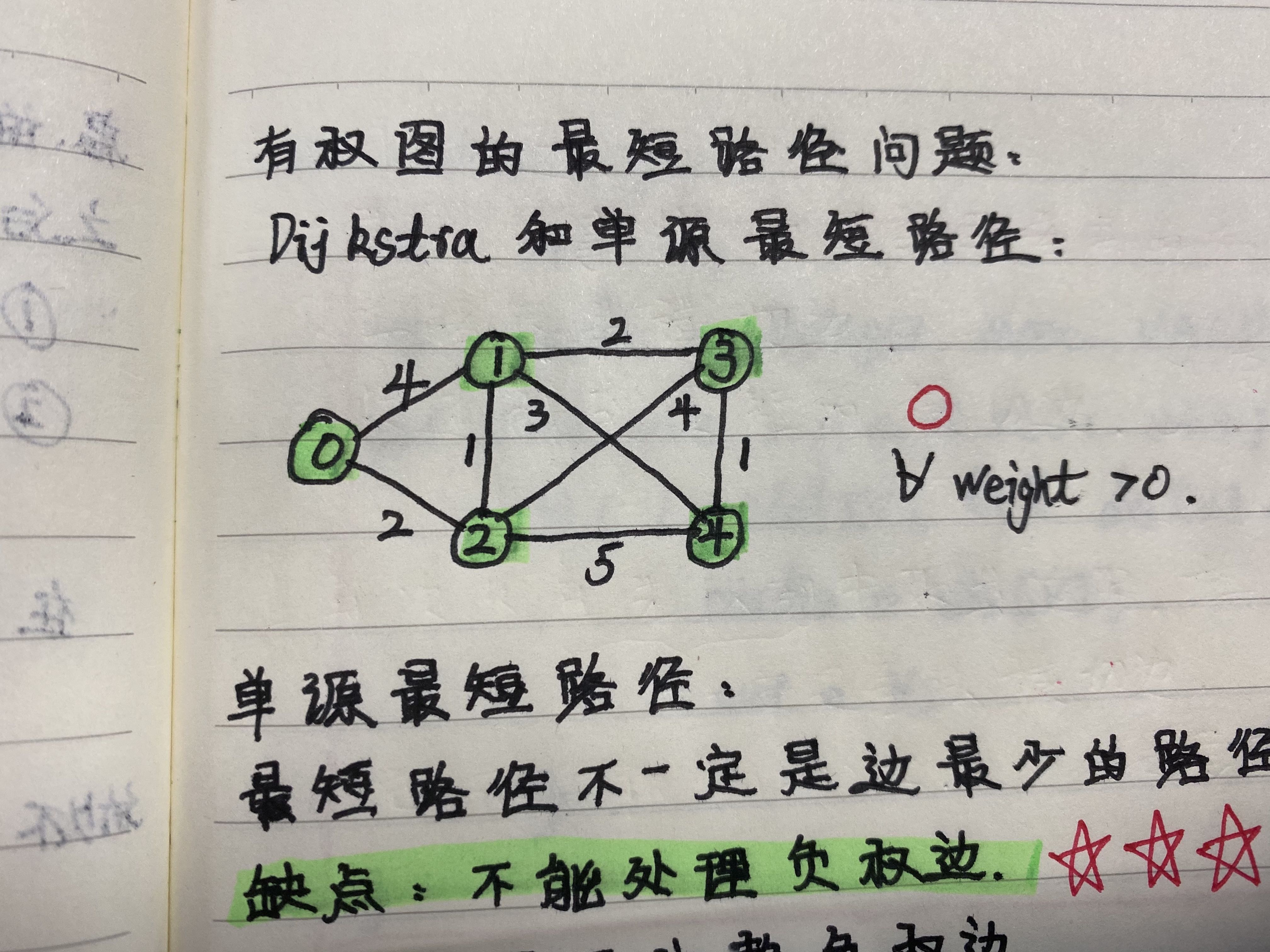
举个例子，我们就看这样的一个简单的图：
0 -> 1 -> 2 -> 3
其中0->1的权值为1；1->2的权值为1；2->3的权值为1。起始点为0；终止点为3。
初始：dist[0] = 0; dist[1] = ∞; dist[2] = ∞; dist[3] = ∞。
在这里注意，我们每轮松弛所有的边，都是从顶点为0的边开始松弛的。
第一轮松弛：
首先，松弛0->1这条边，可以松弛，得到：
dist[0] = 0; dist[1] = 1; dist[2] = ∞; dist[3] = ∞；
0相邻的所有边松弛完了，松弛1相邻的边，即松弛1->2，可以松弛，得到：
dist[0] = 0; dist[1] = 1; dist[2] = 2; dist[3] = ∞；
1相邻的所有边松弛完了，松弛2相邻的边，即松弛2->3，可以松弛，得到：
dist[0] = 0; dist[1] = 1; dist[2] = 2; dist[3] = 3；
至此，我们只用了一轮松弛操作，就得到了从0到3的最短路径。但是，注意，我们之所以只用一轮松弛操作，是基于我们在松弛1->2这条边的时候，恰巧0->1这条边刚刚松弛过，使得使得dist[1]不再是∞；同理，我们在松弛2->3这条边的时候，敲好1->2这条边刚刚被松弛过，使得dist[2]不是∞。
---
下面，我们看这个例子：
3 -> 2 -> 1 -> 0
其中3->2的权值为1；2->1的权值为1；1->0的权值为1。起始点为3；终止点为0。
初始：dist[3] = 0; dist[2] = ∞; dist[1] = ∞; dist[0] = ∞。
第一轮松弛：
首先，0没有邻边，看1的邻边。
松弛1->0这条边，不可以松弛，因为dist[1]=∞！
看2的邻边，2->1这条边，不可以松弛，因为 dist[2]=∞！
看3的邻边，3->2这条边，可以松弛，得到：
dist[3] = 0; dist[2] = 1; dist[1] = ∞; dist[3] = ∞
第一轮松弛结束！
第二轮松弛：
首先，0没有邻边，看1的邻边。
松弛1->0这条边，不可以松弛，因为dist[1]=∞！
看2的邻边，2->1这条边，可以松弛，得到：
dist[3] = 0; dist[2] = 1; dist[1] = 2; dist[3] = ∞
看3的邻边，3->2这条边，可以松弛，得到：
dist[3] = 0; dist[2] = 1; dist[1] = 2; dist[3] = ∞ （在这里是一次重复松弛）
第二轮松弛结束！
第三轮松弛：
首先，0没有邻边，看1的邻边。
松弛1->0这条边，现在可以松弛了，得到：
dist[3] = 0; dist[2] = 1; dist[1] = 2; dist[3] = 3
看2的邻边，2->1这条边，可以松弛，得到：
dist[3] = 0; dist[2] = 1; dist[1] = 2; dist[3] = 3（在这里是一次重复松弛）
看3的邻边，3->2这条边，可以松弛，得到：
dist[3] = 0; dist[2] = 1; dist[1] = 2; dist[3] = 3 （在这里是一次重复松弛）
第三轮松弛结束！
至此，三轮松弛后，我们才能得到从3->0的最短路径。
仔细观察，在这个例子里，每一轮结束后，我们得到就是从src(3)到每个顶点，经过k步后所能得到的最短路径。（∞表示不可抵达）
当然，这个例子比较极端。在实际情况下，还有很多情况，都会让松弛操作1轮不能得到最终答案。虽然松弛一轮可能就得到了答案，但也可能无法得到答案。但松弛V-1轮，是一定可以获得最终答案的。这是最保守的情况。你也可以试试，随机生成一个图，然后将松弛1轮后的结果和松弛V-1轮后的结果比较一下。在大多数情况下，应该都是不同的：）
有意思的是，最近Leetcode上有一道题，题目是求在一个图中，从源点到终点，最多只可以经过k条边的最短路径。由于有“最多只可以经过k条边”这个限制，使用这个课程的这个bellman-ford代码是不可以的，因为我们的代码经过k轮松弛后，可以得出经过大于k条边的最短路径。所以需要再这个代码的基础上进行改进。有兴趣可以自己研究一下：）
题目链接：https://leetcode.com/contest/weekly-contest-72/problems/cheapest-flights-within-k-stops/
我的完成这个问题使用的“改进的”Bellman-Ford代码（C++）：https://github.com/liuyubobobo/Play-Leetcode/blob/master/0787-Cheapest-Flights-Within-K-Stops/cpp-0787/main.cpp
（这里的“改进”加引号，是因为这样做效率其实不优，但是得到题目要求的答案：）
继续加油！：）
相似问题
登录后可查看更多问答，登录/注册
