视频中的疑问，基于size优化后，8←3←4这个树可能出现吗？

Question

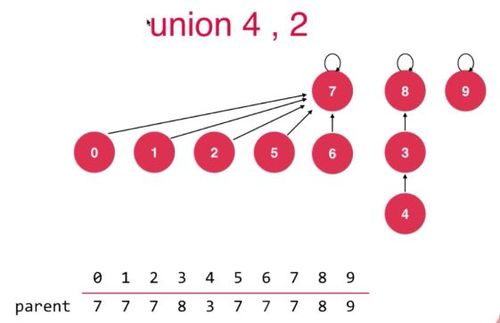
如上图所示，这是本节视频开头演示的基于size优化后可能出现的不利情况。我的疑问是，基于size优化的并查集，真的会出现 8←3←4 这个树吗？

根据定义，在最初阶段，8，3，4是各自独立的元素，出现 8←3←4 这个树唯一可能的步骤是：

1、union 3,4  形成 3←4

2、union 8,4 或 union 8,3 形成 8←3←4

问题出在第2步，当进行size优化后，执行 union 8,4 或 union 8,3 时，会先比较 size(8) 和 size(3)，此时，size(8)=1 而 size(3)=2，程序会将 8 并入 3 之下，形成 3 为根，8 和 4 分别为子节点的情况，也就是说 8←3←4 这种一条线的三层树不可能出现。

进一步推导，size优化后的并查集，出现8←3←4 这种三层的树的一个必要条件是—— 8 必须有其他的子节点，比如说在上图中，如果 9 是 8 的子节点，即存在 8←9 和 3←4 两个树的情况下进行 union 8,3 操作，才会出现 8←3←4 这样的情况。

也就是说，基于size优化的并查集，通常情况下已经能避免形成很多层级的树了，出现极端情况的概率其实不大，不知道我的理解是不是对的？

Answer 1

liuyubobobo 2017-03-09 21:53:10

大赞！你描述的非常对。这里举的例子我只是为了说明这个情况，没有考虑可能性。你的分析非常正确！

不过在实际的生产环境中，也可能存在这样的情况，比如之前产生的树结构基于UF2实现的，后来版本进行了升级，UF的归并逻辑升级成了UF3，但还是有可能要处理由于UF2的逻辑生成的结构数据：）

不过你最终的结论非常对，如果从头实现并查集，基于size的优化和基于rank的优化，效率近乎没差。只不过从理论分析的角度，基于rank比基于size更好一些：）

再赞一次对问题和逻辑的详细描述！：）