leetcode虚拟周赛做到一题，可以使用最大匹配的思路去做，分享一下

Question

leetcode1349-参加考试的最大学生数

对于此题，本人思路参考题解中的LighT二分图最大独立集 的思路，并使用bobo老师课程中书写的匈牙利算法dfs版本对其中有关匹配的部分进行了代码书写。

大致思路如下所示：

1. 由于题目的特殊性，导致奇数列和偶数列形成了二分图中的两个部分

2. 图中蓝色位置表示所有可以坐的位置，只需要对这些位置进行图的建模

3. 对于每个位置，需要将其与它冲突的位置连起来，所谓冲突的位置，即：若有学生坐在此位置，他可能会去偷看别人的试卷，也可能会被后面的人偷看到。对于每个位置，都有六个位置（除边界）需要考虑

4. 为什么这样建模求最大匹配就可以得到答案呢？
   i. 首先每个位置只能坐一个人

   ii. 在图的建模过程中，对于左边每个位置（记作A），我们已经将它与“所有与它冲突的位置”连接起来。即 此时左边位置与它所连接的所有右边位置中，只能选取一个。
   ps：这里有一个小问题可能会比较绕，你可能会觉得此时应该选择A这个位置，而把右边所有与A相连接的位置删掉。而实际上，如果此时与A连接的有多个右边位置的话，我们可以选取任意一个右边位置，而不去选取A。因为这样即便所有与A连接的右边位置与A冲突，然而他们相互之间并不冲突。

   iii. 这样的一条边的选取，就会被记作一个可用的位置

5. 最后应该返回的结果是：所有可用的位置 - 最大匹配数，为什么呢？
   因为最大匹配数，所求出来的是奇数位置和偶数位置中相互冲突的那些位置，这些位置**（本质有左右两个位置）**中只能被选取一个位置。剩下的没有被匹配的位置中，左边位置和右边位置并不冲突（因为他们之间没有连边），所以这些位置我们都要进行选取。
   也就是结果应该是： independent + maxMatching， 而independent = all - 2*maxMatching，代入之后也就得到了 all - maxMatching

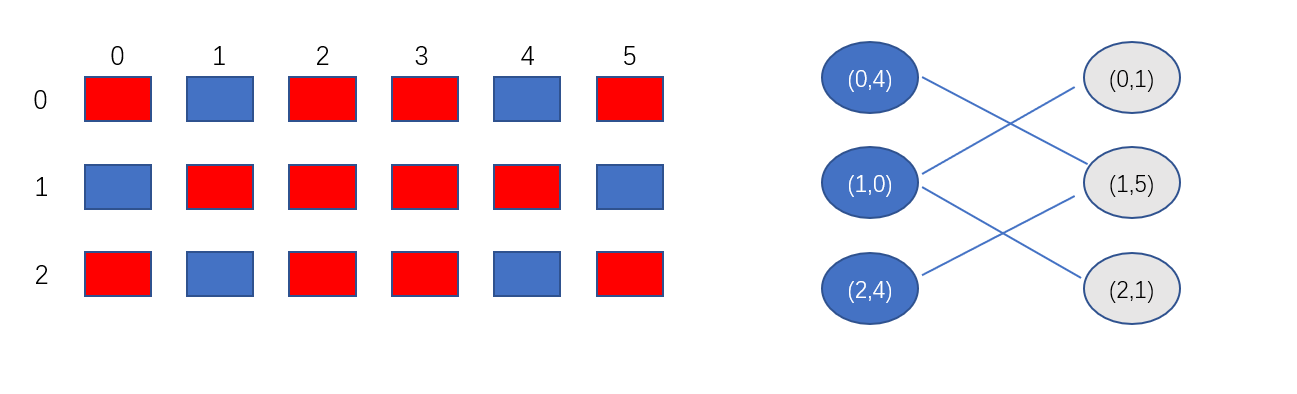
6. 下图是使用题目示例所建出来的二分图，最后就是在这样的图上进行匹配从而得到答案。
   

下面贴出一份个人的实现代码，仅供参考：

class Solution {
    private HashMap<Integer, List<Integer>> g;
    private int m, n;
    private int[] matching;
    private boolean[] visited;
    public int maxStudents(char[][] seats) {
        
        m = seats.length;
        n = seats[0].length;

        matching = new int[m*n];
        Arrays.fill(matching, -1);
        visited = new boolean[m*n];

        //建二分图，由于匈牙利算法的过程只需要从左边的点出发去寻找右边的点
        //所以这里将列号为偶数的假定为左边的点，并只记录从左边点出发所能到达的路径
        g = new HashMap<>();
        int all = 0; //表示所有能坐的座位
        for(int r = 0; r < m; r ++){
            for(int c = 0; c < n; c ++){
                if(seats[r][c] == '.'){
                    all ++;
                    if(c % 2 == 0){
                        int cur = r*n + c;
                        List<Integer> adj = new ArrayList<>();
                        g.put(cur, adj);

                        //作弊别人，左，右，左前，右前
                        if(inArea(r - 1, c - 1) && seats[r - 1][c - 1] == '.')
                            adj.add((r - 1)*n + (c - 1));
                        if(inArea(r - 1, c + 1) && seats[r - 1][c + 1] == '.')
                            adj.add((r - 1)*n + (c + 1));
                        if(inArea(r, c - 1) && seats[r][c - 1] == '.')
                            adj.add(r*n + c - 1);
                        if(inArea(r, c + 1) && seats[r][c + 1] == '.')
                            adj.add(r*n + c + 1);
                        //被别人作弊，左下，右下
                        if(inArea(r + 1, c - 1) && seats[r + 1][c - 1] == '.')
                            adj.add((r + 1)*n + (c - 1));
                        if(inArea(r + 1, c + 1) && seats[r + 1][c + 1] == '.')
                            adj.add((r + 1)*n + (c + 1));
                    }
                }
            }
        }

        int ans = 0;
        //匈牙利算法
        for(int v: g.keySet()){
            Arrays.fill(visited, false);
            if(dfs(v)) ans ++;
        }
        return all - ans;
    }
    
    private boolean dfs(int v){
        visited[v] = true;

        for(int next: g.get(v)){
            if(visited[next]) continue;
            visited[next] = true;
            if(matching[next] == -1 || dfs(matching[next])){
                matching[v] = next;
                matching[next] = v;
                return true;
            }
        }
        return false;
    }

    private boolean inArea(int x, int y){
        return x >= 0 && x < m && y >= 0 && y < n;
    }
}

Answer 1

liuyubobobo 2020-06-11 03:23:10

大赞！感谢分享！：）

这种题解放到 Leetcode 中文区的“题解”里，可能能让更多人阅读到，产生的影响力更大：）

另外，这个问题也能使用动态规划的思路做，可以参考我的代码（C++）：https://github.com/liuyubobobo/Play-Leetcode/blob/master/1349-Maximum-Students-Taking-Exam/cpp-1349/main.cpp

继续加油！：）

• 提问者 martin123_ #1

  感谢老师回复，因为此题正好是一个可能比较难想到的图论建模问题，所以才在问答区分享了。当时本人学习此课程最后两章时，对一个题如何建模成图论问题感觉很苦恼，很需要这方面的练习。所以才分享希望可以帮助一下更多有这种烦恼的同学。

• liuyubobobo 回复 提问者 martin123_ #2

  大赞！感谢分享！：）