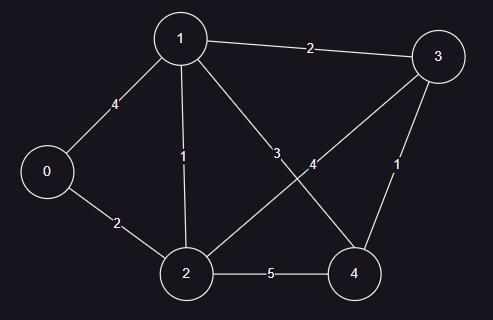
【JS】根据老师讲解Dijkstra算法的模拟过程思路，自己实现了Dijkstra算法。

Question

function dijkstra(graph) {
  let curv = 0;
  let dis = Array(graph.V()).fill(Number.MAX_SAFE_INTEGER);
  let visited = Array(graph.V()).fill(false);
  //! 需遍历的顶点数
  let count = graph.V();

  //! 1.确定一个点
  dis[curv] = 0;
  visited[curv] = true;
  --count;

  while (count > 0) {
    //! 距离curv最邻近的顶点
    let minw = -1;
    //! 距离curv最邻近的顶点距离
    let minDis = Number.MAX_SAFE_INTEGER;
    //! 2.根据确定点，更新相邻点的距离
    for (const w of graph.adj(curv)) {
      if (visited[w]) {
        continue;
      }
      dis[w] = Math.min(dis[w], dis[curv] + graph.getWeight(curv, w));
      if (dis[w] < minDis) {
        minw = w;
        minDis = dis[w];
      }
    }
    //! 3.遍历结束后，设置其中的最短边，作为下一个确定点
    if (minw != -1) {
      //! 4.再次执行1过程，直到所有顶点都遍历完成
      curv = minw;
      visited[curv] = true;
      --count;
    } else {
      console.log("已找不到最邻近距离点：", `curv:${curv},minw:${minw}`);
      break;
    }
  }

  for (let i = 0; i < graph.V(); i++) {
    console.log(`0-${i}:`, dis[i]);
  }

  return dis;
}

let res = dijkstra(new WeightedGraph(resolve(__dirname, "g.txt")));
console.log(res);

输出结果：

0-0: 0
0-1: 3
0-2: 2
0-3: 5
0-4: 6
[ 0, 3, 2, 5, 6 ]

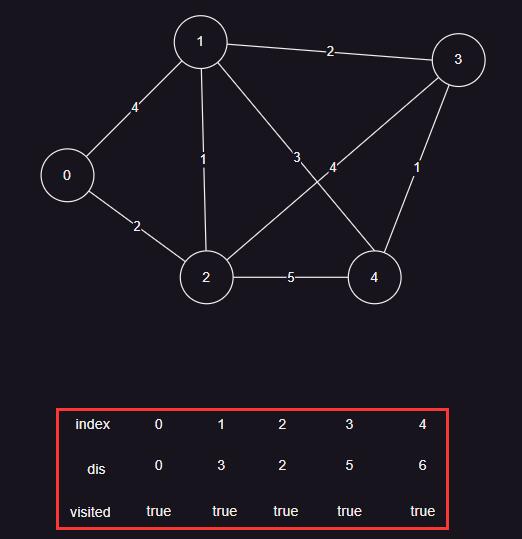
测试这个图没有问题，请问老师我这实现有问题吗？

---

由于自己回答自己的问题，系统提示老师和同学看不到，所以把答案贴到下面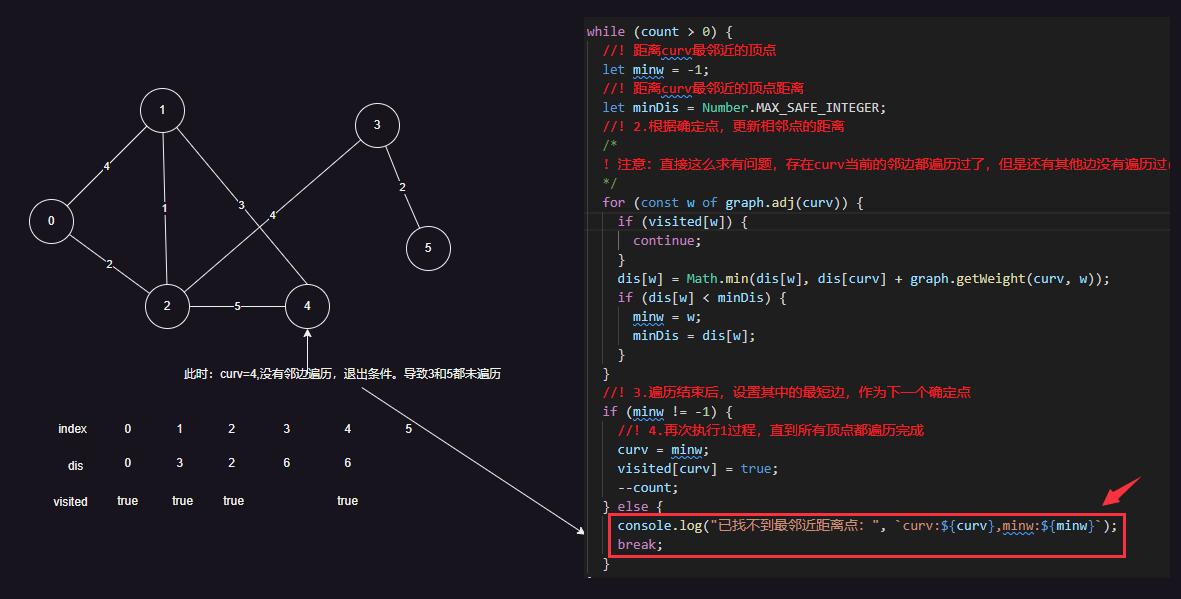

此时：curv=4,没有邻边遍历，退出条件。导致3和5都未遍历，所以还是得在前面加一段逻辑，从剩余的点遍历找最短距离的点，再走下面的逻辑。

Answer 1

liuyubobobo 2023-05-18 22:21:00

感谢分享。

力扣中有大量 dijkstra 相关的问题，比如这个问题：https://leetcode.com/problems/network-delay-time/ 可以用类似这样的问题测试自己的算法。

继续加油！：）