关于老师对于LR先对X左旋转转化成了LL的说法
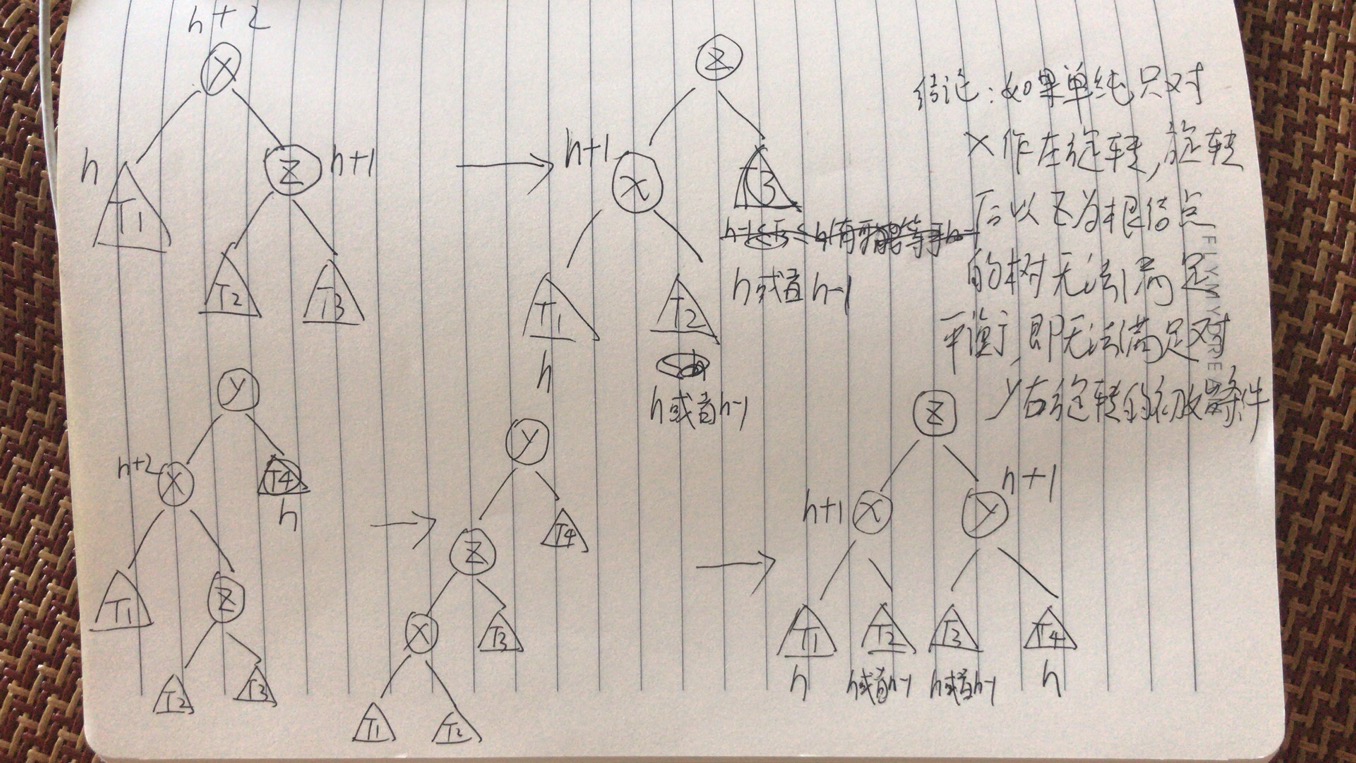
当对X进行左旋转后,新的y的以Z为根节点的左子树有可能是不平衡的,这就打破了对Y进行右旋转的初始条件,但是我发现最后对于Y进行右旋转的结果的确是满足平衡的,所以我认为在这里不能说是先转换成了LL的情况而应该说将两个步骤合在一起最终使LR的情况达到平衡,不知道老师对于我的这种思考怎么看呢
1821
收起

当对X进行左旋转后,新的y的以Z为根节点的左子树有可能是不平衡的,这就打破了对Y进行右旋转的初始条件,但是我发现最后对于Y进行右旋转的结果的确是满足平衡的,所以我认为在这里不能说是先转换成了LL的情况而应该说将两个步骤合在一起最终使LR的情况达到平衡,不知道老师对于我的这种思考怎么看呢