请稍等 ...

【JS】欧拉路径实现(回溯实现、栈实现)

方式1：回溯实现

function findEulerPath(graph) {
    let cc = new CC(graph);
    if (cc.cccount() != 1) {
      return [];
    }

    let startv = 0;
    let cnt = 2;
    for (let i = 0; i < graph.V(); i++) {
      if (graph.degree(i) % 2 != 0) {
        cnt--;
        startv = i;
      }
    }

    //! 说明：如果存在2个以上度<2的顶点，就不存在欧拉路径，直接返回
    if (cnt < 0) {
      return [];
    }

    let E = graph.E();
    let res = [];
    let count = 0;

    function print(...args) {
      // console.log("-".repeat(count), ...args);
    }

    function dfs(v, path) {
      count++;
      path.push(v);
      //! 说明：当前的边数全部遍历完，说明找到解
      if (graph.E() == 0) {
        res = path.slice(0);
        print("find solution: ", res);
        return true;
      }

      //! 说明：需要把当前顶点的相邻顶点copy出来，如果不copy出来就会导致for循环的是循环。for里面不能边删除又添加
      let edges = [...graph.adj(v).values()];

      for (const w of edges) {
        //! 遍历操作
        graph.deleteEdge(v, w);

        print("push:", path);

        if (dfs(w, path)) {
          return true;
        }

        //! 回溯操作
        graph.addEdge(v, w);
        path.pop();

        print("pop:", path);
      }

      count--;
      return false;
    }

    for (let i = 0; i < graph.V(); i++) {
      if (i != startv) {
        continue;
      }
      let isFindPath = dfs(i, []);
      if (isFindPath) {
        return res;
      }
    }

    return [];
  }

  let res = findEulerPath(new Graph(path.resolve(__dirname, "./assets/g0.txt")));
  console.log(res.join("->"));

  res = findEulerPath(new Graph(path.resolve(__dirname, "./assets/g.txt")));
  console.log(res.join("->"));

方式2：利用栈实现

 function findEulerPath(graph) {
    let cc = new CC(graph);
    if (cc.cccount() != 1) {
      return [];
    }

    let startv = 0;
    let cnt = 2;
    for (let i = 0; i < graph.V(); i++) {
      if (graph.degree(i) % 2 != 0) {
        cnt--;
        startv = i;
      }
    }

    //! 说明：如果存在2个以上度<2的顶点，就不存在欧拉路径，直接返回
    if (cnt < 0) {
      return [];
    }

    let g = graph.clone();
    let res = [];
    let stack = [];
    let curv = startv;
    stack.push(curv);

    while (stack.length != 0) {
      if (g.degree(curv) != 0) {
        let w = g.adj(curv).values().next().value;
        stack.push(curv);
        g.deleteEdge(curv, w);
        curv = w;
      } else {
        res.push(curv);
        curv = stack.pop();
      }
    }

    return res;
  }

  let res = findEulerPath(new Graph(path.resolve(__dirname, "./assets/g0.txt")));
  console.log(res.join("->"));

  res = findEulerPath(new Graph(path.resolve(__dirname, "./assets/g.txt")));
  console.log(res.join("->"));

测试数据

g0.txt

图片描述

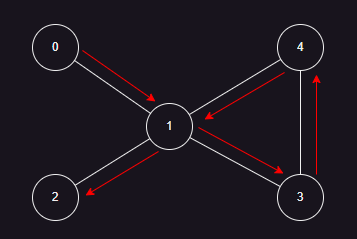
测试结果：

-------------------------------------1.回溯法-----------------------------
2->1->3->4->1->0
-------------------------------------2.Hierholzer - 栈实现-----------------------------
0->1->4->3->1->2

g.txt

图片描述

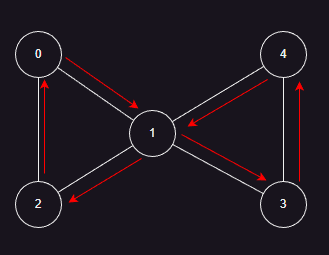
-------------------------------------1.回溯法-----------------------------
0->1->3->4->1->2->0
-------------------------------------2.Hierholzer - 栈实现-----------------------------
0->2->1->4->3->1->0

栈的实现，求欧拉路径和欧拉回路，仅仅只是加了一段边的合法校验+startv遍历起始点，其他代码就是欧拉回路栈实现代码，请问老师我的实现有问题吗？

Potter520 2023-05-12 21:41:47

源自：10-7 欧拉路径和本章小结

269

收起