PCA降维后精度下降很多

Question

老师你好，我在用PCA做数据降维的时候出现了这种情况，原始数据有3000多个维度，PCA降维设置保留95%信息量，然后降维直接就降到3维，我看了一下数据，数据的各个维度确实相关性很大，然后用降维之后的数据做测试，发现降维后的数据比降维前的数据精度下降了很多，按道理来说不应该降低太多啊，这一般是什么原因呢？我的数据分布如下：

![图片描述](http://img1.sycdn.imooc.com//szimg/63120aca0840b00214201152.jpg

Answer 1

liuyubobobo 2022-09-03 06:53:41

这是可能的，PCA 不能保证精度的上升。

最典型的例子，一个数据在高维空间是线性可分的，但是降到低维空间，可能就不再线性可分了。也正是因为这个原因，是存在“升维”的算法的。比如多项式回归。SVM 从原理上也在升维，只是升的维度直接从特征的角度看不出来而已。

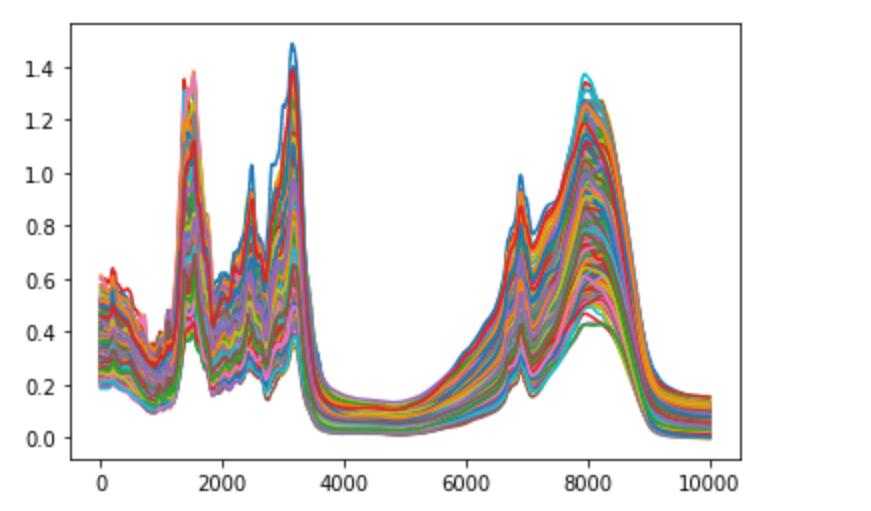
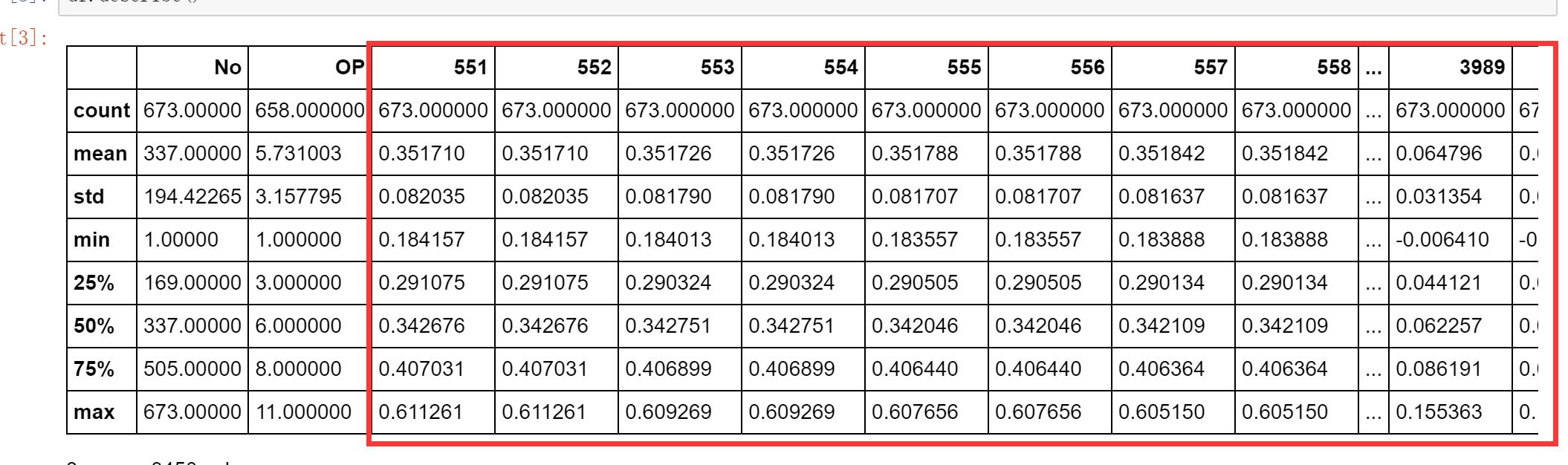
这点在高维数据其实会更明显。尤其如果你的样本量不够大。对于高维数据，维度灾难很容易形成。比如你的原始数据是 3000 维，这意味着什么？这意味着在 3000 维的空间中，从（0,0,0,0, ..., 0） 到 （1, 1, 1, ..., 1），也就是 3000 维空间的一个单元格上，就有 2^3000 这么多个点！（每个维度可以取 0 或者 1）。这个数字是什么概念？宇宙中原子总数不过 2^300 这个级别左右。也就是一个 3000 维的空间的单元格的顶点上，能够轻松装下宇宙中的所有的原子，还有一多半的富余空间。

在这么高维的空间中，数据会显得非常稀疏，以至于能很好地区分它们。在这种情况下，降维会使得区分它们变困难。因为随着维度的降低，空间越来越狭小，数据点越来越“挤在”一起，他们之间的关系就变得越来越“难以描述”。

所以降维降多少维是一个 trade-off，保留的维度太少，数据丢失的信息过多；保留的空间过多，维度灾难越来越严重。

==========

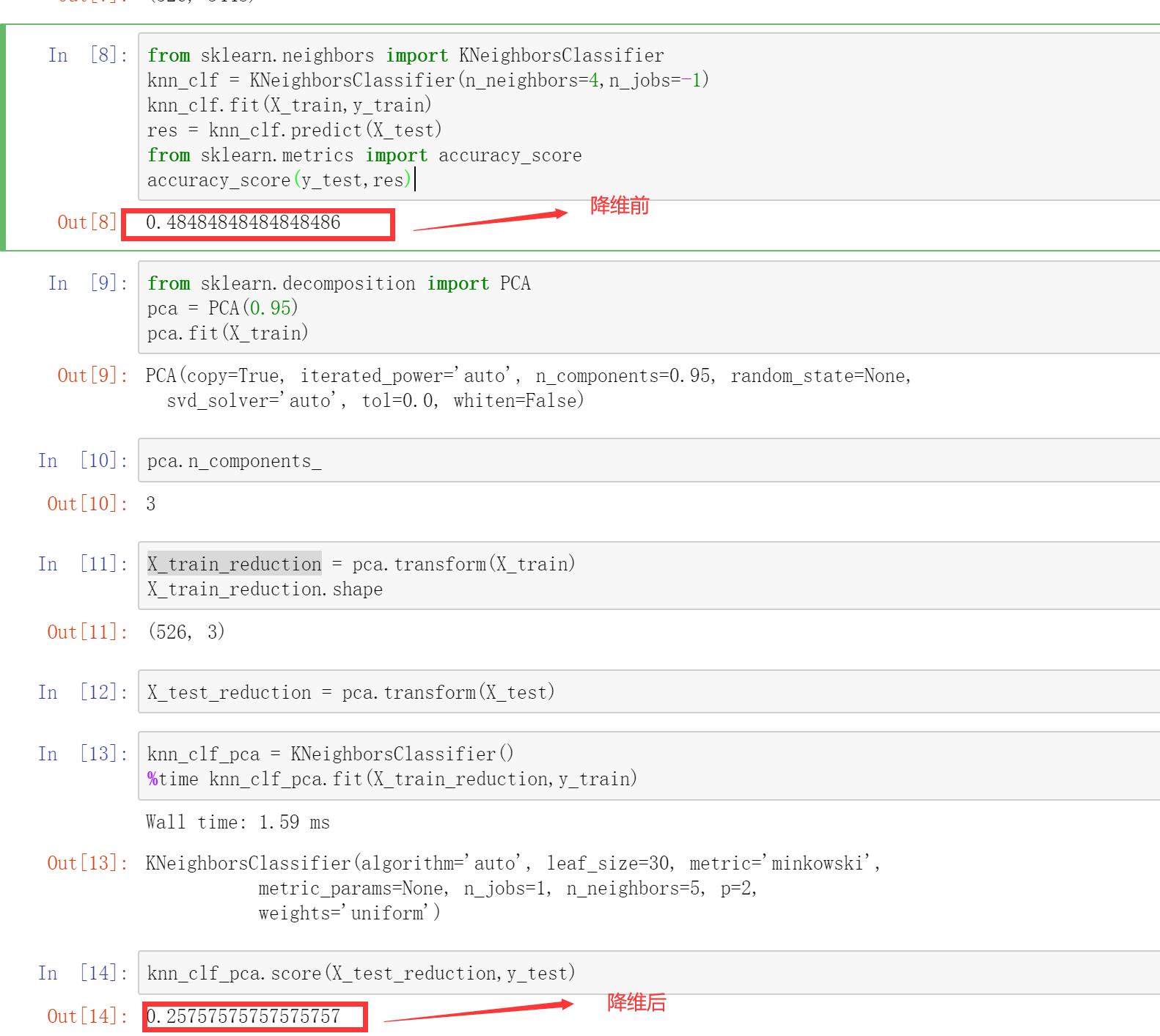
但是，在这里，一个非常重要的思维（也是做机器学习的一个重要的思维）是：准确度降低，不代表你的模型不好。这里的模型的好不好，不是说模型的准确率低不低，而是说你的模型是不是“合理”，是不是真的反映了他的预测能力。

在我看来，如果保留了 95% 的信息，你的数据变成三维，用 knn 得到的准确率是 25%，但是在 3000 维的数据下，准确率是 48%，我更倾向于认为，使用 knn 模型，在你的数据下，得到的 25% 准确率是更可信的。

对于这方面的讨论，可以参考这个问答：

https://coding.imooc.com/learn/questiondetail/2vGBEPxZGdzXNkaq.html

以及这个问答的 2）：

https://coding.imooc.com/learn/questiondetail/vZnjEY773L0Y72Wd.html

继续加油！：）

• 提问者 linux小爬虫 #1

  收到，谢谢老师