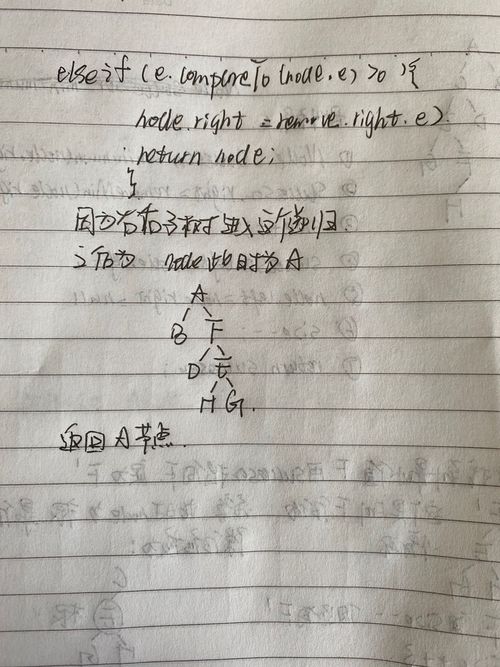关于面试
老师您好，我有回来了，上次看到这里的时候我提问了一个问题
这个时候我的学习就是看着视频1.5倍速，看完视频简单理解加上看的认真，代码细节就记下来额。然后背着写下课程的代码。然后就结束了，以为这样就可以了。然后重数组到Tree，越到后面就越吃力，因为前面的代码都是背下来的，缺乏自己的理解。等到后面多个知识点一起运用的时候，对数据和方法的理解，递归的理解都不是很好。这次我又从第二章重新看了一遍，放慢倍速，在老师讲完将要实现算法的的思想后，在写代码之前，我会根据算法的思想，去代码实现，然后单步调试，用纸笔去写去思考。当然，也会遇到不对的，遇到不对的就接着看视频，看看老师如何实现，对比老师的实现，我的问题在哪里，如果我实现的对了，也会看一遍，加深印象。同时我看完后会在去看下《漫画算法》这本书，根据课程的讲解，找到对应的章节，在看下数据结构这部分，最后，在找些简单的leetcode的算法，加固一下学习。
第一遍看到第六章可能我只学会了20%，那这次应该可以达到70%。因为还是有的不理解，感觉很绕。但是这次之前的leetcode困惑的问题有些可以自己搞定了，有的看别人的解法加上找资料，可以理解更多了一点，虽然还是有很多不理解，但是要好很多，信心和积极性也要高了。
谢谢老师上次对我的回复。这次我也把课程中第六章，说的算法都非递归实现了，还有之前最困扰我的就是这部分代码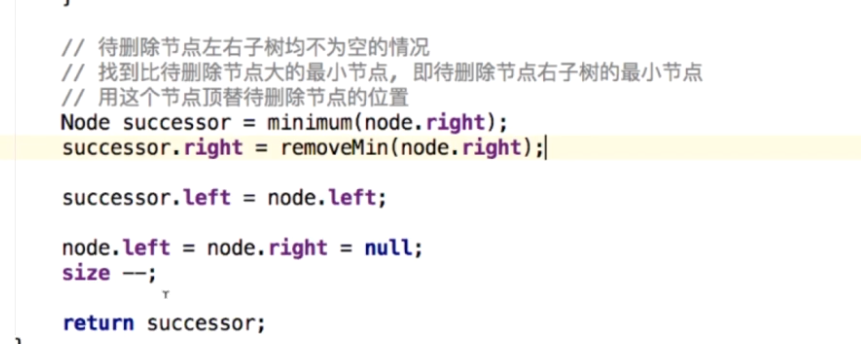
我到现在也没太明白，不过我有了自己的理解，还希望老师帮我看下。在我的基础上，分析下我的分析对嘛！理解的哪里有问题？
还有一个问题，我买了老师的两个课程还有一个玩转算法面试-- Leetcode真题分门别类讲解 ，我是一个工作2年多的Android，想继续找Android，马上就要面试了，因为还有别的要看，我现在看到第六章，为了面试这2个课程我改如何看，上班以外的空闲时间20天我要看完本课程第六章以后的本分，加上另一个课程我该为了面试如何选取。
最后附上非递归实现代码
public class BST<E extends Comparable<E>> {
private class Node {
public E e;
private Node left;
private Node right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
@Override
public String toString() {
return e.toString();
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void add(E e) {
//非递归
if (root == null) {
root = new Node(e);
} else {
Node cur = root;
while (true) {
if (cur.e.compareTo(e) < 0) {// 在右子树上
if (cur.right == null) {
cur.right = new Node(e);
size++;
return;
} else {
cur = cur.right;
}
} else if (cur.e.compareTo(e) > 0) {//再左子树上
if (cur.left == null) {
cur.left = new Node(e);
size++;
return;
} else {
cur = cur.left;
}
} else {
return;
}
}
}
//递归写法
// if (root == null) {
// root = new Node(e);
// }else {
// add(root, e);
// }
}
public boolean contains(E e) {
Node cur = root;
if (cur == null)
return false;
while (cur != null) {
if (cur.e.equals(e)) {
return true;
} else if (cur.e.compareTo(e) > 0) {//在左子树上
cur = cur.left;
} else {//进入这个条件一定是在右子树上
cur = cur.right;
}
}
//如果在循环中没有返回 那么一定是没有找到 那么这里返回false
return false;
//递归实现
// return contains(root, e);
}
private boolean contains(Node root, E e) {
if (root == null) {
return false;
}
if (root.e.equals(e)) {
return true;
} else if (root.e.compareTo(e) > 0) {//在左子树上
return contains(root.left, e);
} else {// (root.e.compareTo(e) < 0) 一定是在右子树上
return contains(root.right, e);
}
}
private Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (node.e.compareTo(e) < 0) {// 在右子树上
node.right = add(node.right, e);
} else if (root.e.compareTo(e) > 0) {//再左子树上
node.left = add(node.left, e);
}
return node;
}
/**
* 前序遍历
*/
public void preOrder() {
preOrder(root);
}
/**
* 前序遍历的非递归遍历
*/
public void preOrderUn() {
if (root == null) {
return;
}
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node node = stack.pop();
System.out.println(node.e);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
private void preOrder(Node root) {
if (root == null) {
return;
}
System.out.println(root.e);
preOrder(root.left);
preOrder(root.right);
}
/**
* 递归中序遍历
*/
public void inOrder() {
inOrder(root);
}
private void inOrder(Node root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.println(root.e);
inOrder(root.right);
}
public void inOrderUn() {
inOrderUn(root);
}
private void inOrderUn(Node root) {
if (root == null) {
return;
}
Stack<Node> stack = new Stack<>();
stack.push(root);
Node cur = root;
while (!stack.isEmpty()) {
while (cur.left != null) {
stack.push(cur.left);
cur = cur.left;
}
Node pop = stack.pop();
System.out.println(pop.e);
if (pop.right != null) {
stack.push(pop.right);
cur = pop.right;
}
}
}
/**
* 递归后序遍历
*/
public void postOrder() {
postOrder(root);
}
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
public void postOrderUn() {
postOrderUn(root);
}
/**
* https://blog.csdn.net/qq_39445165/article/details/90749343?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
* <p>
* 非递归后序遍历
*
* @param root
*/
private void postOrderUn(Node root) {
Stack<Node> src = new Stack<>();
Stack<Node> pos = new Stack<>();
src.push(root);
while (!src.isEmpty()) {
Node pop = src.pop();
pos.push(pop);
if (pop.left != null) {
src.push(pop.left);
}
if (pop.right != null) {
src.push(pop.right);
}
}
while (!pos.isEmpty()) {
System.out.println(pos.pop().e);
}
}
/**
* 查找二分搜索树的最小值
*/
public E minimum() {
if (size == 0) {
throw new IllegalArgumentException("空树");
}
return minimum(root).e;
}
/**
* 循环查找
*
* @param root
* @return
*/
private Node minimum(Node root) {
if (root.left == null) {
return root;
}
return minimum(root.left);
}
/**
* 查找最大值
*/
public E maximum() {
if (size == 0) {
throw new IllegalArgumentException("空树");
}
return maximum(root).e;
}
private Node maximum(Node root) {
if (root.right == null) {
return root;
}
return maximum(root.right);
}
/**
* 删除最小值
*/
public E removeMin() {
E e = minimum();
removeMin(root);
return e;
}
/**
* 删除掉以node为根的二分搜索树中的最小节点
* 返回删除节点后新的二分搜索树的根
* <p>
* TODO 删除最大节点逻辑相同
*/
private Node removeMin(Node root) {
if (root.left == null) {//进入这个分支说明找到了最小节点 就是root
//这时候root.right可能为空 但是不影响逻辑
Node rightNode = root.right;
//将带删除的root节点 right的这指向 为null
root.right = null;
//此时递归进入 是已root为根节点 那么 新的根节点就是rightNode;
size--;
return rightNode;
}
//递归最后 返回的是此时根节点的左子树的最小值已经删除掉了 那么此时根节点的左子树就是返回来的新的节点
//如果是空的话 也是正确的
root.left = removeMin(root.left);
//最后返回递归结束的根节点 就是删除最小值的根节点
return root;
}
public E removeMax() {
E e = maximum();
removeMax(root);
return e;
}
private Node removeMax(Node root) {
if (root.right == null) {
Node leftNode = root.left;
root.left = null;
size--;
return leftNode;
}
root.right = removeMax(root.right);
return root;
}
/**
* 删除任意元素
*/
public void remove(E e) {
remove(root, e);
}
/**
* 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
* 返回删除节点后新的二分搜索树的根
*/
private Node remove(Node node, E e) {
if (node == null) {//循环到最后都没有找到e元素
return null;
}
if (e.compareTo(node.e) > 0) {//元素在右子树上
//这个方法本身是删除以root为节点后的根据节点 因为传入的是右子树
// 那么此时节点的右子树 应该接上删除节点后的根节点
node.right = remove(node.right, e);
//然后返回这个根节点
return node;
} else if (e.compareTo(node.e) < 0) {//元素在左子树上
//同上
node.left = remove(node.left, e);
//然后返回这个根节点
return node;
} else {//e==node.e 找到了这个节点 那么判断删除节点是否有子节点
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
//返回去 这是的rightNode因为在右节点上 那么比e要大 所以进入(e.compareTo(node.e) < 0)这个分支
//然后用node.left接上 再一直递归返回
return rightNode;
}
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
//返回去 这是的rightNode因为在右节点上 那么比e要大 所以进入(e.compareTo(node.e) < 0)这个分支
//然后用node.left接上 再一直递归返回
return leftNode;
}
//都没有return返回 走到这里 说明 左右子树都不是空
//最小节点存起来
Node successor = minimum(node);
successor.right = removeMin(node.right); //查找右子树的最小节点 这里也可以换成查找左子树的最大节点
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public int maxDepth(Node root, int left, int right) {
if (root == null) {
return 0;
}
left = maxDepth(root.left, left + 1, right);
right = maxDepth(root.right, left, right + 1);
return Math.max(left + 1, right + 1);
}
/**
* 二分搜索树的层序遍历
*/
public void levelOrder() {
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
Node cur = q.remove();
System.out.println(cur.e);
if (cur.left != null)
q.add(cur.left);
if (cur.right != null)
q.add(cur.right);
}
}
public int maxDepth() {
return maxDepth(root, 0, 0);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
outputDepth(root, 0, res);
return res.toString();
}
private void outputDepth(Node node, int depth, StringBuilder res) {
if (node == null) {
String s = output(depth) + "null\n";
res.append(s);
return;
}
res.append(output(depth)).append(node.e).append("\n");
outputDepth(node.left, depth + 1, res);
outputDepth(node.right, depth + 1, res);
}
private String output(int depth) {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < depth; i++) {
builder.append("--");
}
return builder.toString();
}
public static void main(String[] args) {
// int[] arr = {12, 3, 6, 9, 5, 2, 8, 15};
int[] arr = {5, 3, 6, 4, 2};
// int[] arr = {9, 5, 3, 7, 6, 8};
// int[] arr = {6, 12, 19, 18, 17, 21, 20};
BST<Integer> bst = new BST<>();
for (int i = 0; i < arr.length; i++) {
bst.add(arr[i]);
}
System.out.println(bst);
System.out.println(bst.contains(0));
System.out.println("==========递归前序遍历");
bst.preOrder();
System.out.println("==========非递归前序遍历");
bst.preOrderUn();
System.out.println("==========");
System.out.println("==========递归中序遍历");
bst.inOrder();
System.out.println("==========非递归中序遍历");
bst.inOrderUn();
System.out.println("==========");
System.out.println("==========递归后序遍历");
bst.postOrder();
System.out.println("==========非递归后序遍历");
bst.postOrderUn();
System.out.println("==========");
System.out.println("Depth======" + bst.maxDepth());
System.out.println("==========查找最小值");
System.out.println(bst.minimum());
System.out.println("==========查找最大值");
System.out.println(bst.maximum());
System.out.println("==========删除最小节点");
bst.removeMin();
bst.inOrder();
System.out.println("==========删除最大节点");
bst.removeMax();
bst.inOrder();
System.out.println("==========删除任意节点");
bst.inOrder();
System.out.println("=========");
bst.remove(6);
bst.inOrder();
}
}
利用递归来实现链表的所有操做
/**
* 利用递归来实现链表的所有操做
*/
public class DummyLinkedList<E> {
private class Node {
public E e;
public Node next;
public Node(E e) {
this.e = e;
next = null;
}
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
@Override
public String toString() {
return e.toString();
}
}
private Node dummyHead;
private int size;
public DummyLinkedList() {
dummyHead = new Node(null);
size = 0;
}
public DummyLinkedList(E e) {
dummyHead = new Node(null);
dummyHead.next = new Node(e);
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void add(int index, E e) {
if (index < 0 || index > size) {//size指向的是最后一个元素的下一个元素 那么index=size表示向尾部添加元素
throw new IllegalArgumentException("下标越界");
}
add(dummyHead, index, 0, e);
}
/**
* @param head 头节点
* @param index 用户要插入的index
* @param current 表示 当前执行到那个index
* @param e 要插入的元素
*/
private void add(Node head, int index, int current, E e) {
if (current == index) {
size++;
head.next = new Node(e, head.next);
return;
}
add(head.next, index, current + 1, e);
}
public void addFirst(E e) {
add(0, e);
}
public void addLast(E e) {
add(size - 1, e);
}
public E remove(int index) {
return remove(dummyHead, index, 0);
}
private E remove(Node head, int index, int current) {
if (current == index) {
Node delNode = head.next;
head.next = head.next.next;
delNode.next = null;
return delNode.e;
}
E e = remove(head.next, index, current + 1);
return e;
}
public E removeFirst() {
return remove(0);
}
public E removeLast() {
return remove(size - 1);
}
public void set(int index, E e) {
set(dummyHead.next, index, 0, e);
}
private void set(Node head, int index, int current, E e) {
if (current == index) {
head.e = e;
return;
}
set(head.next, index, current + 1, e);
}
public boolean contains(E e) {
return contains(dummyHead.next, e);
}
private boolean contains(Node head, E e) {
if (head == null) {
return false;
} else {
if (head.e.equals(e)) {
return true;
}
}
return contains(head.next, e);
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
for (Node node = dummyHead.next; node != null; node = node.next) {
builder.append(node.e).append("->");
}
builder.append("NULL");
return builder.toString();
}
public static void main(String[] args) {
DummyLinkedList<Integer> linkedList = new DummyLinkedList<>();
for (int i = 0; i < 3; i++) {
linkedList.addFirst(i);
System.out.println(linkedList);
}
linkedList.addFirst(333);
System.out.println(linkedList);
linkedList.add(2, 666);
System.out.println(linkedList);
linkedList.remove(2);
System.out.println(linkedList);
System.out.println(linkedList.contains(333));
System.out.println(linkedList.contains(555));
}
}
602
收起
正在回答 回答被采纳积分+3
2回答
liuyubobobo
2020-03-23 01:51:16
