非常好的问题:)
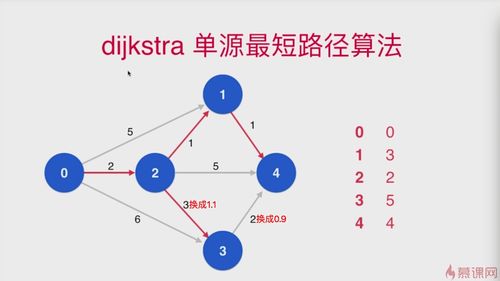
其实你的问题有两个。第一个问题,当将2—3 3—4的权值改成1.1 和 0.9的时候,此时,相当于从0到4的最短路径虽然长度仍然是4,但是其实有两条路径的长度为4。我们现在的dijkstra算法一定能找到其中的一条路径。其实我们可以改造我们的算法找到所有的最短路径,有兴趣可以思考一下看?代码会比较繁琐,在这个课程中就不仔细讲了。有时间我可以在这个课程的github中实现一下这个代码供大家参考。
第二个问题是这个课程涉及的。如果2-3的权值是1.01,3-4的权值是0.09,我们的dijkstra算法是如何找到最短路径的?其实最简单的方法是根据课程介绍的思路手动模拟一遍。或者把这个测试用例放在代码上实际跟踪一下。在这里,我简单的做一下这个事情,看看下面的过程你能否理解?
初始化
0 - 0
1 - 无穷
2 - 无穷
3 - 无穷
4 - 无穷
所以,从起始点(0号节点)到0号节点的距离是最短的,我们的算法会标记,从0号节点到0号节点的最短路径已经找到了。然后对0节点的所有邻边做relax操作。也就是看经过0节点到其他端点,是否有比现在已经找到的最短距离更好的路径?由于初始化的时候我们到其他节点的距离都是无穷,所以所有的0节点的邻边都会被relax。我们就得到了下面的结果:
0 - (0)
1 - 5
2 - 2
3 - 6
4 - 无穷
注意,这个表的意思是,此时,我们找到的从0到0的最短距离为0;从0到1的最短距离为5;从0到2的最短距离为2,从0到3的最短距离为6;从0到4的最短距离为无穷。
这里,0节点的0我用小括号括上,表示是已经找到了的最短路径。那么现在,剩下的[5,2,6,无穷]中,最小值是2,所以我们标记找到了从起点0到节点2的最短路径,之后对节点2的所有邻边进行relax操作
0 - (0)
1 - 3 // 我们有了节点2的最短路径2,从节点2再到节点1只需要2+1=3的长度,比原来的5要小
2 - (2)
3 - 3.01 // 我们有了节点2的最短路径2,从节点2再到节点3只需要2+1.01=3.01的长度,比原来的6要小
4 - 7 // 通过节点2,节点4可达了,其长度为2+5=7
现在,剩下的[3,3.01,无穷]中,最小值是3,所以我们标记找到了从起点0到节点1的最短路径,之后对节点1的所有邻边进行relax操作
0 - (0)
1 - (3)
2 - (2)
3 - 3.01 // 我们有了节点1的最短路径3,从节点1再到节点3需要3+1=4的长度,比3.01大,所以保留3.01
4 - 4 // 我们有了节点1的最短路径3,从节点1再到节点4只需要3+1=4的长度,比原来的7要小
注意,现在算法还没有运行完,剩下的[3.01,4]中,最小值是3.01,所以我们标记找到了从起点0到节点3的最短路径,之后对节点3的所有邻边进行relax操作
0 - (0)
1 - (3)
2 - (2)
3 - (3.01)
4 - 3.1 // 我们有了节点3的最短路径3.01,从节点3再到节点4只需要3.01+0.09=3.1的长度,比原来的4要小
现在,我们就剩下了一个节点4,其他节点的最短路径已经找到了,也就不需要对节点4进行relax操作了。那么这个3.1,就是dijkstra算法找到的最短路径。
我们课程的代码中,使用了索引堆,来加快这个每次取出最小值的过程,同时可以方便快速的在找到一个节点的最短路径后,对这个节点的邻边进行松弛操作,进而更新其他节点的信息。
希望对你有帮助。自己动手画画看,会理解的更深入哦。然后实际的在我们的代码中跑一跑,看一看每次循环的过程,我们的数据是怎样改变的,是一个很好的学习过程哦:)