题目描述：谈谈一些能用数学证明的反直觉的现象。
老师观点：其实有很多能用数学证明的反直觉的现象，我这里举一个生活中的例子，权当抛砖引玉了。这个例子会用到贝叶斯公式，我这里不展开讲贝叶斯公式，对贝叶斯公式不太清楚的，可以自行了解一下，也可以关注我后续的课程。
举例：假设在小明生活的城市对某种疾病进行普查，假设根据以往其他城市的数据，这种疾病的患病率为0.01%，假设医疗机构对患者有98%的概率能够检测出来，再假设医疗机构对正常人有0.2%的概率将正常人诊断为患者，通过这次检查，小明被查出是患者，那么大家觉得小明患病的真实概率有多大。
很可能大家会觉得，小明患病的概率非常大，因为根据假设，医疗机构对患者有98%的概率能够检测出来，会盯着这个98%，但是我告诉大家，根据这些假设条件，小明患病的概率其实小于5%。这个结论是不是有点反直觉。下面我们用贝叶斯公式计算一下。
记A表示该城市的某人真的患病,根据假设，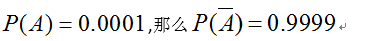
B表示检测结果为患病，注意包含两种情况，一种是将真患者检测成患者，根据假设，对应的概率为

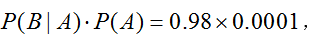
另一种是将正常人检测成患者，根据假设，对应的概率为
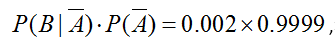根据全概率公式，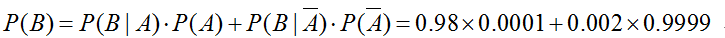
我们现在要计算的是在检测结果为患病的条件下，真实的患病概率，即是求条件概率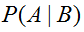 根据贝叶斯公式: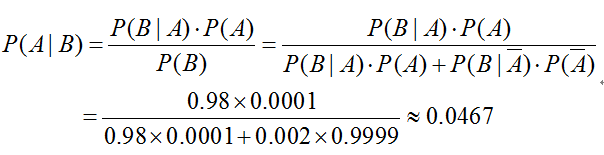
也许大家会觉得不可思议，这个结果确实有点反直觉，会让人觉得检测结果“不太靠谱”，大家可能会有疑问，那咱们平时到医院看病的检测结果真的有这么“不靠谱”吗？其实不是的，一般来说，到医院看某种病的人很可能出现了相应的症状，换句话说，到医院看该病的人真正患该病的概率是比较大的，也就是说这里的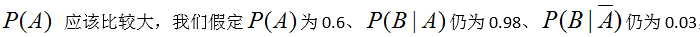

这种情况下，我们计算出,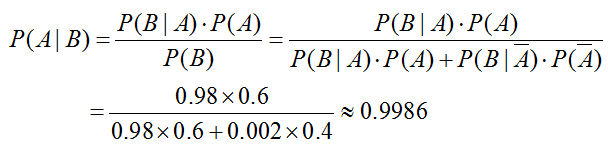

这个结果就基本与我们的直觉相符了。
大家体会到贝叶斯公式的神奇之处了吗。这里只是展示了贝叶斯公式的非常简单的应用，其实贝叶斯公式在机器学习方面也有应用，这方面的内容也将出现在我们规划的课程中，欢迎大家关注。