关于9.4节的Bellman-Ford算法
这个BellmanFord算法是不是要要求从节点s开始能到达所有的结点?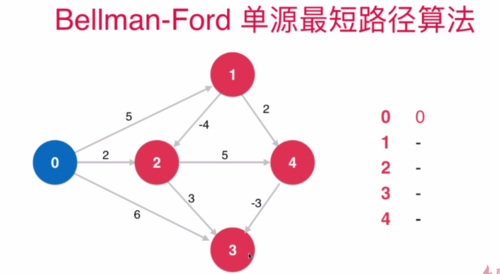
当我对这张图以节点3作为源调用BellmanFord算法的时候,运行出来,程序提示存在负权环。(使用的是已经勘误了的代码)
825
收起
这个BellmanFord算法是不是要要求从节点s开始能到达所有的结点?
当我对这张图以节点3作为源调用BellmanFord算法的时候,运行出来,程序提示存在负权环。(使用的是已经勘误了的代码)