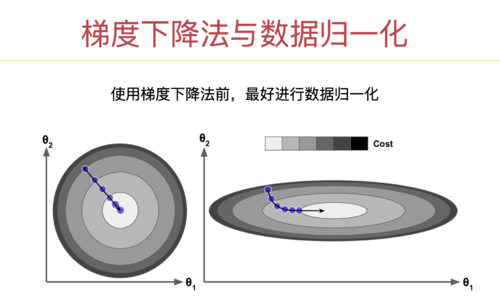
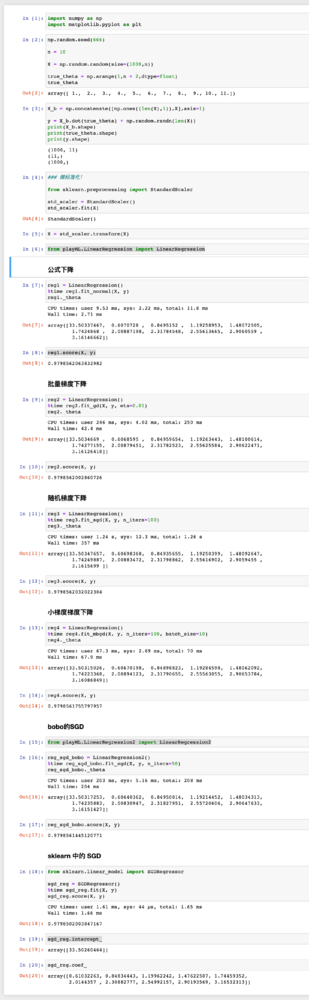
关于随机梯度下降法和小批量梯度下降法实现中的问题
我在这一单元的尾声尝试实现公式法，批量梯度下降法，随机梯度下降法，小批量梯度下降法，在特征量增大，或者训练量增大的情况下，效率会产生什么样的变化，以此来探究不同算法的应用场景。
但是我调试了很久，随机梯度下降法和小批量梯度下降法的结果差强人意。
波波老师能帮我看一下吗？
python代码：
import numpy as np
from .metrics import r2_score
class LinearRegression:
def __init__(self):
"""初始化多元线性回归模型"""
#初始化截距coef_和系数interception_，和theta私有化参数
self.coef_ = None
self.intercept_ = None
self._theta = None
self.history_j = []
#公式法
def fit_normal(self, X_train ,y_train):
assert X_train.shape[0] ==y_train.shape[0],\
"the size of X_train must be equal to the size of y_train"
#ones(多少个,0or1行和列)
X_b = np.concatenate(([np.ones((len(X_train), 1)), X_train]), axis=1)
self._theta = np.linalg.pinv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
#批量梯度下降法
def fit_gd(self,X_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
# 计算J的值
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
# 计算J的导数
def dJ(theta, X_b, y):
reg = np.array(X_b.dot(theta) - y).dot(X_b)
return reg * 2 / len(X_b)
# return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def gradient_descent(X_b, y,initial_theta, eta, n_iters=1e4, epsilon=1e-8):
# 初始化，theta的值，运行次数的值，theta历史的数字
theta = initial_theta
i_iter = 0
# 运行次数超过1万次就退出循环条件1
while i_iter < n_iters:
# 求导数
gradient = dJ(theta, X_b, y)
# 赋值历史theta，用于判断退出循环条件2
last_theta = theta
# 梯度下降，
theta = theta - eta * gradient
# 推出条件，J与上一个J的值差距小于1e-8
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
# 用于记录运行次数
i_iter += 1
return theta
# 合并，在X前插入全1向量
X_b = np.concatenate([np.ones((len(X_train), 1)), X_train], axis=1)
# 随机化系数
initial_theta = np.array(np.random.randint(1, 100, X_b.shape[1]))
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters, epsilon)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
#随机梯度下降法
def fit_sgd(self,X_train, y_train, n_iters=5, t0=5, t1=50):
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert n_iters >= 1,\
'n_iters must big to 1'
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.dot(X_b_i.dot(theta) - y_i) * 2
# eta不用传了，应为由tot1和循环次数决定
def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b)
for cur_iter in range(n_iters):
indexs = np.random.permutation(m)
X_b_new = X_b[indexs,:]
y_new = y[indexs]
for i in range(m):
grandient = dJ_sgd(theta, X_b_new[i], y_new[i])
theta = theta - learning_rate(cur_iter * m + i) * grandient
return theta
# 合并，在X前插入全1向量
X_b = np.concatenate([np.ones((len(X_train), 1)), X_train], axis=1)
# 随机化系数
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
def fit_mbgd(self, X_train, y_train, n_iters=5, batch_size=10 , t0=5, t1=50):
assert X_train.shape[0] == y_train.shape[0], \
"the size of X_train must be equal to the size of y_train"
assert n_iters >= 1, \
'n_iters must big to 1'
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dJ_mbgd(theta, X_b_b, y_b):
return X_b_b.T.dot(X_b_b.dot(theta) - y_b) * 2 / len(y_b)
# eta不用传了，应为由tot1和循环次数决定
def mbgd(X_b, y, initial_theta, n_iters=5, batch_size=10, t0=5, t1=50):
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b)
for cur_iter in range(n_iters):
indexs = np.random.permutation(m)
X_b_new = X_b[indexs, :]
y_new = y[indexs]
b_iters = m // batch_size
b_lost = m % batch_size
#运行整数倍的次数
for i in range(b_iters):
star_sub = i * batch_size
end_sub = (i + 1) * batch_size
#print(star_sub,':',end_sub)
grandient = dJ_mbgd(theta, X_b_new[star_sub:end_sub], y_new[star_sub:end_sub])
theta = theta - learning_rate(cur_iter * m + i) * grandient
#对剩下的余数进行操作
#假如i运行到最后一次，再把余下的几个数也带入运算
if i == b_iters - 1 and b_lost != 0:
star_sub = m - b_lost
end_sub = m
#print(star_sub, ':', end_sub)
grandient = dJ_mbgd(theta, X_b_new[star_sub:end_sub], y_new[star_sub:end_sub])
#外部循环总次数+这一次循环的平均值
theta = theta - learning_rate(cur_iter * m + (star_sub+end_sub) // 2) * grandient
return theta
# 合并，在X前插入全1向量
X_b = np.concatenate([np.ones((len(X_train), 1)), X_train], axis=1)
# 随机化系数
initial_theta = np.random.randn(X_b.shape[1])
self._theta = mbgd(X_b, y_train, initial_theta, n_iters,batch_size, t0, t1)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
def predict(self,X_predict):
assert self.intercept_ is not None and self.coef_ is not None,\
'must fit before predict'
assert X_predict.shape[1] == len(self.coef_),\
'the feature number of X_predict must be equal to X_train'
X_b = np.concatenate([np.ones((len(X_predict),1)),X_predict], axis=1)
return X_b.dot(self._theta)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression()"
jupyter Notebook代码：
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.random(size=(1000,10))
true_theta = np.arange(1,12,dtype=float)
true_theta
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
X_b = np.concatenate([np.ones((len(X),1)),X],axis=1)
y = X_b.dot(true_theta) + np.random.randn(len(X))
print(X_b.shape)
print(true_theta.shape)
print(y.shape)
(1000, 11)
(11,)
(1000,)
from nike.LinearRegression import LinearRegression
公式下降
reg1 = LinearRegression()
%time reg1.fit_normal(X, y)
reg1._theta
CPU times: total: 31.2 ms
Wall time: 279 ms
array([ 1.06235692, 2.06140404, 2.92905058, 4.13374737, 5.06223164,
5.91565075, 6.98756913, 8.01091582, 8.87663003, 9.99713526,
10.91864727])
公式法对于小特征的数据，算的非常快，很准确
批量梯度下降
reg2 = LinearRegression()
%time reg2.fit_gd(X, y, eta=0.01)
reg2._theta
CPU times: total: 1.53 s
Wall time: 1 s
array([ 1.08149657, 2.05888109, 2.92483628, 4.12923291, 5.05851957,
5.91239648, 6.98337669, 8.00786151, 8.87221152, 9.99377222,
10.91456707])
随机梯度下降
reg3 = LinearRegression()
%time reg3.fit_sgd(X, y, n_iters=50)
reg3._theta
CPU times: total: 625 ms
Wall time: 630 ms
array([ 2.92996755, 1.82083214, 2.52998165, 3.70049877, 4.71769946,
5.60161382, 6.56538012, 7.71122574, 8.45391087, 9.65767321,
10.50330375])
随机梯度下降循环50次都运算的比批量梯度下降快，效率很高，但不知道是不是我实现有问题，
小梯度梯度下降
reg4 = LinearRegression()
%time reg4.fit_mbgd(X, y, n_iters=1000,s=10)
reg4._theta
CPU times: total: 2.12 s
Wall time: 2.15 s
array([6.45852788, 2.32447243, 2.56591601, 2.88825355, 4.59566197,
5.15786023, 5.33734587, 6.77725766, 7.7695783 , 7.86900782,
9.04487576])
就是对于theta第一个数，也就是**intercept_**截距，我觉得很疑惑，怎么会这么奇怪呢，我调试了很多次还是有问题，波波老师能帮我看一下吗？
正在回答
1回答
我简单实验了一下。你的实现基本没有问题。你得到的结果不够好的核心原因，是在 Jupyter Notebook 的调用上。
我不确定我在课程中是否强调过了。对于梯度下降法，对数据做标准化，不仅会提高搜索的效率，更重要的是，能够提高搜索的精度。因为标准化讲数据的每一个维度的尺度统一了。我简单搜索了一下，就是这页 ppt 的内容。（或许是我强调的不够。）
这一点当数据维度上升的时候，将表现得越来越明显。如果不同尺度的数据规模不统一，顺着一个梯度方向走一步，在不同的维度上，走的实际“距离”就不一样。维度越高，这个偏差的积累就越大，导致了结果的不精确。
当然，这种不精确可以通过调整学习率相关的参数来“校正”，但是最佳的解决方案，是做一遍标准化。
批量梯度下降法由于其梯度的方向是 100% 准确的，所以对这个问题表现得不明显。但是在有“随机”的梯度下降法中（sgd 和小批量梯度下降），因为每次梯度的方向是不准确的，所以就会更多的收这个问题的影响。
==========
以下的 Jupyter Notebook 的内容，是我在本地，使用你的代码做的实验。你可以看到，四种方法的结果都是一致的。
但是注意，因为对数据标准化以后，数据的尺度变了，所以得到的系数和你预设的系数是不一致的。但是其预测能力是不变的。
对于每个调用，我都用 score 验证其 r^2 值（接近 1 说明是准确的。）
最终，我使用我在课程中实现的 sgd 和 sklearn 中的 sgd 也跑了同样的数据，和你的代码是一致的，说明是准确的。
大赞一下实验精神！
继续加油！：）
相似问题
登录后可查看更多问答，登录/注册
