【疑惑】决策边界的生成，SVM与多项式的关系

Question

https://coding.imooc.com/learn/questiondetail/237493.html

在消化波波老师这段话的时候，关于数据升维之后，将更可能线性可分这一点我有了比较深刻的认识，但在我深入思考后对于决策边界我产生了很多疑惑，我发现这部分我还不是很清楚。

---

疑惑（一）

以下是我在整理多项式进行逻辑回归时的思想历程，也是我疑惑的开始。

1. 对X数据进行多项式（升维）
2. 对X数据进行归一化（数据处理）
3. 通过逻辑回归建立模型（建模）
4. 通过模型预测，从而得出决策边界（可视化）

就多项式逻辑回归而言，决策边界的得到是在建立模型之后，通过模型的预测得到的，从多项式来看决策边界有接触到（通过高维数据建立的模型）高维数据(多项式后的X),但是SVM高斯核函数似乎并没有对数据进行升维，直接结合公式求结论，我的疑惑在于: 决策边界究竟是在二维层面画出一个很复杂的曲线（没升维），还是在高维简单的图像映射到低维的结果？

---

疑惑（二）

这个疑惑承接上文，和我上次问的PCA有些类似

假设（我更倾向于这个可能）决策边界是高位映射到低维的结果，在1维的数据X升维到2维，用一条线进行线性可分；2维数据X升到3维，是用一条线进行分割？还是用一个二维平面进行分割？
以此类推k维数据升到n维，是用n-1维进行分割还是？还是用一条直线进行分割？

---

疑惑（三）(不重要)

关于SVM中的核函数和多项式与决策边界的关系

二者在生成决策边界的过程中有何不同？

• 从结果来看，都生成了非线性的决策边界
• 从生成的结果来看，高斯核函数似乎呈圆形，多项式呈分割状。
  
  

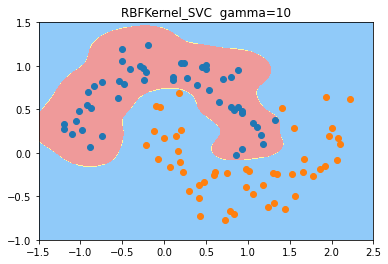
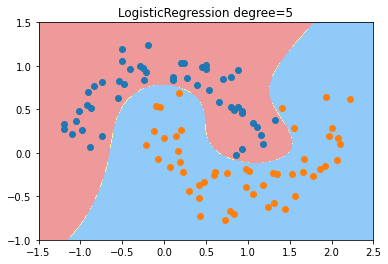
#高斯核函数
Pipeline([
        ('std',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

#多项式
Pipeline([
        ('Poly',PolynomialFeatures(degree=degree)),
        ('standard',StandardScaler()),
        ('linearSVC',LinearSVC(C=C))
    ])

我不清楚二者之间的核心区别，亦或者区别不大？

Answer 1

liuyubobobo 2022-09-06 02:04:53

1）

决策边界究竟是在二维层面画出一个很复杂的曲线（没升维），还是在高维简单的图像映射到低维的结果？

在任何维度的空间里，都存在决策边界的概念。只不过在二维空间中更容易可视化而已。

说白了，决策边界是一个“点集”，这个“点集”中的所有的点，被分到 A 类别或者 B 类别的“概率”是相等的。在二维空间中，决策边界就构成了一条“曲线”；在三维空间，决策边界会构成一个“曲面”，在四维空间，决策边界将构成一个“曲体”，以此类推。

2）

在1维的数据X升维到2维，用一条线进行线性可分；2维数据X升到3维，是用一条线进行分割？还是用一个二维平面进行分割？
以此类推k维数据升到n维，是用n-1维进行分割还是？还是用一条直线进行分割？

广义来讲，在 n 为空间，线性可分是指可以被一个 n - 1 维的“平面”分开。这被称为是“超平面”。

3）

简单来说，多项式特征（或者多项式核）和高斯核都是在做升维，只是升维的方式不同。

多项式核实如何升维的，非常简单，不多说了。

高斯核实际把原始特征升成的形式是什么样子的？因为背后的数学推导有些麻烦，所以我在课程中没有介绍，但如果你感兴趣，这页 PPT 包含了相关推导（来源：https://www.csie.ntu.edu.tw/~cjlin/talks/kuleuven_svm.pdf  ）

继续加油！：）

• 提问者 黄义舜 #1

  1）太精辟了，我要做笔记“决策边界是一个“点集”，这个“点集”中的所有的点，被分到 A 类别或者 B 类别的“概率”是相等的。”
  2）第二个问题，我在看第一问的时候也明白了。
  3）嗯，好的，我周末看看能不能学习到一些，创新的思路。
  4）谢谢bobo老师，我这门课可能快学完了，很感谢能遇到您，并陪我走一段路。假如以后我还在坚持的话，希望有朝一日能和您“华山论剑”。

• liuyubobobo 回复 提问者 黄义舜 #2

  看好你，加油哇！：）