“导数是可以表示方向的,对应J增大方向”这点没看懂
波波老师你好。损失函数J=(x-2.5)^2 -1,你在视频中是这么讲的:“当theta增加时,J是减小的,当theta减小时,J是增加的”。这点我能明白,然后得出结论是:“从某中意义上讲,导数是可以代表方向,对应J增大的方向,想得到J的最小值, 必须在导数前面乘以-eta”。这中间的逻辑,没想明白。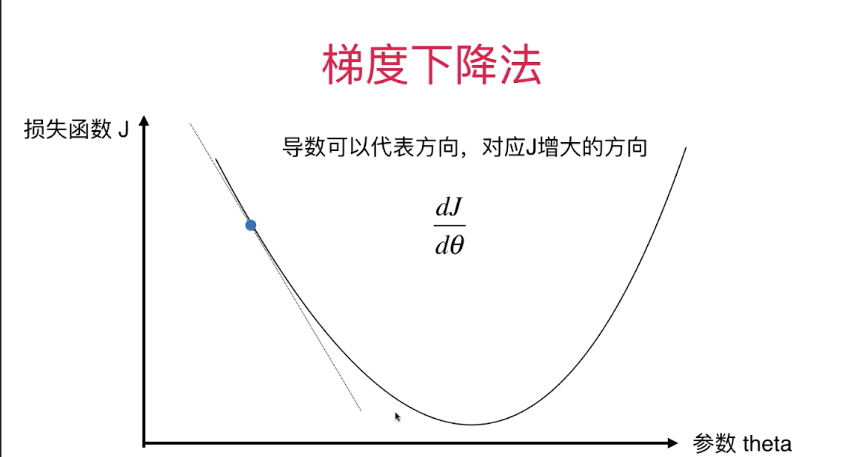
2564
收起
波波老师你好。损失函数J=(x-2.5)^2 -1,你在视频中是这么讲的:“当theta增加时,J是减小的,当theta减小时,J是增加的”。这点我能明白,然后得出结论是:“从某中意义上讲,导数是可以代表方向,对应J增大的方向,想得到J的最小值, 必须在导数前面乘以-eta”。这中间的逻辑,没想明白。