在这里问一下老师有关LCA的相关问题......由于今天奥赛在讲树上倍增LCA问题时不是很理解这种问题......
对于LCA(Least Common Ancestors)这类问题，其实就是求一个树中任意两点的最近的公共父节点。
其本人对其理解，先检查两节点的深度是否为同一深度，若不为同一深度，则将深度大的节点进行往上提，使其两点的深度为一致。这仅仅只是第一步，接下来，就是要使两个节点同时往上跳，可以一个一个地往上跳，使其到达第一个使这两点合并为一点的公共父节点，也是最近父节点。但一个一个跳则数据太的话，就非常耗时，于是引入了位运算中的“<<”（其实就是以2^i的形式进行倍增式跳跃），其作用就是使两点以倍增的形式往上跳，这样比一个节点以个节点地跳要省时好多，但是就引起了以下的思考：
1，如果跳到最后，两个点都跳越界了呢.....就是跳出来该树的根节点以外呢？
2，如果以倍增的形式进行上跳，如何知道它们倍增往上跳的时候跳的他们父父父父父的父节点是哪个呢？看到网上都是定义了一个二维的int数组，如：int fa[max][max],然后用fa[i][0]表示第i个节点的父节点，fa[i][1]表示第i个节点的父节点的父节点，以此类推，然后就可以得到一个递推式：fa[i][j]=fa[fa[i][j-1]][j-1]，其文字叙述就是i的第2^j个父亲 是i的第2^(j-1)个父亲的第2^(j-1)个父亲。QAQ什么鬼......
3，整张图以邻接表的形式进行建图吗？那如何建呢？想过用vector来模拟邻接表，也想过用一维数组来表示，但是，有点力不从心，关键在某博客里看到定义了一个一维的vector却TM可以用二维数组的方式来表示里面的数据.....
4，用DFS对depth[n]进行赋值的话，Emmmmmmm好吧，本人会去复习一下DFS的（其实就是对图的遍历吧）.....
5，在把两个节点给弄到同一深度时，有着一串代码：
if(depth[a] < depth[b]) swap(a, b);
int c = depth[a] - depth[b];
for(int i = 0; i <= 14; i++){
if(c & (1 << i)){
a = up[a][i];
}
}
其中的if(c & (1 << i))这个判断条件不是很懂......
不知道老师怎么看待这个LCA问题.......谢谢老师QAQ
正在回答
2回答
整体看了一遍你的问题，你的一些问题暴露出了你的基础其实还不够。在玩儿奥赛的同时，一定要补足基础。在奥赛上获得好成绩，都是建立在坚实的基础上的。没有好的基础，一方面对很多更难的算法将很难理解，甚至无法理解；另一方面，即使从数学的角度理解了算法，具体实现起来也举步维艰：）（更不用提，如果没有具体实现做基础，很多自以为正确的“理解”，很有可能是不全面的，甚至是错误的。）
你的问题中，有些根本和LCA无关，有些则是LCA的这个算法特有的问题。由于LCA问题不是这个课程的内容，我也不可能在一篇问答里就把LCA问题彻底讲清楚。所以只针对你现有的问题做一些简单的回答，请谅解。希望我的回答可以帮助你查缺补漏：）
问题3：
树本身就是一个特殊的图，是有n个节点，n-1条边，且所有的n个节点组成了一个联通分量的图。所以用图的表示法表示树当然可以。在树中v是u的孩子节点，就可以对应图中(u, v)一条边。（根据需要看是有向边还是无向边，一般有向边就ok）
至于邻接表使用vector，也近乎是最常见的实现。在我们这个课程中就是这样做的。请看7-3的代码：https://github.com/liuyubobobo/Play-with-Algorithms/blob/master/07-Graph-Basics/Course%20Code%20(C%2B%2B)/03-Vertex%20Adjacent%20Iterator/SparseGraph.h
第20行，我们的图使用vector<vector<int>> g表示，g就是一个二维数组；
比如第58行（g[v][i] == w），我们就是在判断节点v的第i个相邻节点是否为w：）
问题4：
DFS是基础中的基础。不要说奥赛了，在面试问题中都属于基础问题。作为计算机专业，必须极其熟练。在这个课程中，对于树的DFS和图的DFS，我都介绍了，可以再回顾一下：）
奥赛应该有DFS的专项训练问题，从最简单的开始刷20道先。如果DFS都不熟悉，不应该接触这个LCA问题：）
问题5：
位运算确实是我在这个课程上没有涉及的（我在慕课网上所有的课程都暂时没有涉及），同时，对于玩儿竞赛的同学，一定要掌握的内容。无论是BIT，还是状态压缩DP，RMQ，等等，都会涉及位运算，甚至很多问题本身都直接基于位运算。
在网络上搜索“位运算”（或者Google搜索英文"Bit Manipulation"或者"Bitwise Algorithms"），应该有不少零散的文章，帮助你理解基本位运算的基本含义。比如这些文章可以扫一遍：https://www.geeksforgeeks.org/bitwise-algorithms/#basics
如果想更深刻的理解位运算，就需要动手实践了，扫一遍Leetcode上和位运算相关的练习是很有帮助。遇到不会的就直接去看discuss里大家的讨论和题解，都做下来，位运算的使用基本就没问题了。上面的链接中geeksforgeeks的很多文章都配相应的习题。Leetcode也是一个很好的地方，Leetcode中位运算相关的练习：https://leetcode.com/tag/bit-manipulation/
具体你的代码中，c & (1 << i)，就是看c的第i个比特位是否为1，在这里的意义是看2^i是否小于等于c。
问题2：
从这个问题开始，才是真正的和这个LCA算法相关的问题：）
i的第2^j个父亲 是i的第2^(j-1)个父亲的第2^(j-1)个父亲很好理解啊。我们随便带一个j：
比如j = 1，就是说i的第2个父亲 是i的第1个父亲的第1个父亲，也就是i的祖父是i的父亲的父亲；
比如j = 2，就是说i的第4个父亲 是i的第2个父亲的第2个父亲，就是先向上走两步，再向上走两步，就等于向上走四步；
比如j = 3，就是说i的第8个父亲 是i的第4个父亲的第4个父亲，就是先向上走四步，再向上走四步，就等于向上走八步；
以此类推：）
这也揭示了在理解复杂算法的时候，一个非常非常重要的方法，不要只是对着算法的代码，或者课本上抽象的揭示生看硬想！用一个小的测试用例，带进去，看看到底怎么回事儿！在这里，我建议，先不要管后面的LCA过程，就先仔细研究一下这个fa数组。用一个小的测试用例，比如只有个位数的节点的数据，实际跑一下，一点一点跟踪一下，看看这个fa数组是怎样一点一点赋值，每次fa[i][j]赋值成了多少，结合自己的数据用例，具体的看为什么会赋值成这个样子。这是理解算法的非常重要的工作！切不可犯懒！通常花费一个下午，仔仔细细的跟踪一边算法，钻进算法里跑一遭，你的收获，要高于对着这段话想一个礼拜，甚至一个月！在理解算法这件事情上，没有捷径。使用具体的例子，是最好的理解方式。即使有人给你讲明白，近乎一定是靠例子给你讲明白的。而举例子，看看对于具体的例子，算法内部到底发生了什么，自己就可以做！
问题1：
如果你手里已经有了LCA的代码，那么他一定不会越界。依然是，用一个具体的例子（用一个你觉得会越界的例子更好），具体的跑一遍算法，看看你的算法是否越界了？如果没有越界，到底是哪里处理了这个边界情况？为什么没有越界？自己哪里没有想到或者想错了？依然是，用具体的测试用例跟进算法内部，是学习算法的最好的方式！
加油！
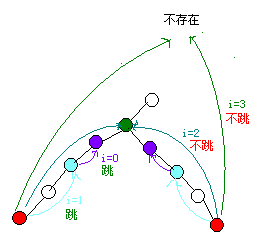这是其中当倍增跳的时候跳出界的情况.......
相似问题
登录后可查看更多问答，登录/注册
