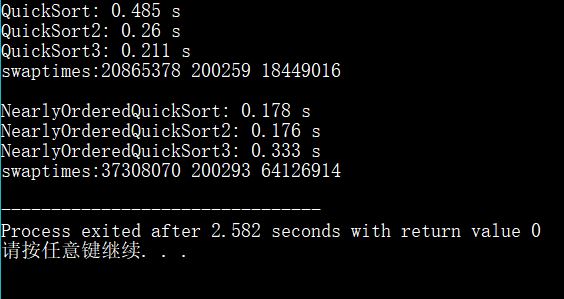
为什么我的三路快排在无序数组排序的时候性能好于两路快排？

Question

#include
#include
#include

#include"SortTestHelper.h"
#include"MergeSort.h"
#include"InsertionSort.h"

using namespace std;

int count1=0,count2=0,count3=0; //比较一下交换次数

template //已经改为随机快排
int Partition(T arr[],int l,int r) {
swap(arr[l],arr[rand()%(r-l+1)+l]); //随机交换头和其中一个元素
T aux=arr[l];
int i,j=l;
for(i=l+1; i<=r; i++) {
if(arr[i]<aux) {
j++;
swap(arr[j],arr[i]);
count1++;
}

}
swap(arr[l],arr[j]);
count1++;
return j;

}

template
int Partition2(T arr[],int l,int r) {
swap(arr[l],arr[rand()%(r-l+1)+l]); //随机交换头和其中一个元素
T aux=arr[l];
int i=l+1,j=r,lt,gt;
while(true){
while(i<=r&&arr[i]<aux) i++; //为什么不能是等于呢？
while(j>=l+1&&arr[j]>aux) j–; //为什么不能是等于呢？

	if(i>j){
		break;
	}
	swap(arr[i],arr[j]);
	count2++;
	i++;
	j--;
}



swap(arr[l],arr[j]);
count2++;
return j;

}

template
void __QuickSort(T arr[],int l,int r) {
if(r-l<=15) {
BetterInsertionSort(arr,l,r);
return; //判断递归终止的条件
}
int p=Partition(arr,l,r);
__QuickSort(arr,l,p-1);
__QuickSort(arr,p+1,r);
}

template //两路快排
void __QuickSort2(T arr[],int l,int r) {
if(r-l<=15) {
BetterInsertionSort(arr,l,r);
return; //判断递归终止的条件
}
int p=Partition2(arr,l,r);
__QuickSort(arr,l,p-1);
__QuickSort(arr,p+1,r);
}

template //三路快排
void __QuickSort3(T arr[],int l,int r) {
if(r-l<=15) {
BetterInsertionSort(arr,l,r);
return; //判断递归终止的条件
}
swap(arr[l],arr[rand()%(r-l+1)+l]);
int i=l+1,j=r,lt=l,gt=r+1; //注意每一个变量的定义
T aux=arr[l];
while(i<gt){
if(arr[i]<aux){
swap(arr[lt+1],arr[i]);
count3++;
lt++;
i++;
}else if(arr[i]>aux){
swap(arr[i],arr[gt-1]);
count3++;
gt–;
}else{
i++;
}
}

swap(arr[l],arr[lt]);
count3++;
__QuickSort3(arr,l,lt-1);
__QuickSort3(arr,gt,r);

}

template //由普通的基本快排优化到随机快排
void QuickSort(T arr[],int n) {
srand(time(NULL));
__QuickSort(arr,0,n-1);
}

template //随机的两路快排
void QuickSort2(T arr[],int n) {
srand(time(NULL));
__QuickSort2(arr,0,n-1);
}

template //随机的三路快排
void QuickSort3(T arr[],int n) {
srand(time(NULL));
__QuickSort3(arr,0,n-1);
}

int main() {

int n=1000000;
int *arr2=SortTestHelper::generateNearlyOrderedArray(n,100); 
int *arr4=SortTestHelper::copyArray(arr2,n);
int *arr6=SortTestHelper::copyArray(arr2,n);

int *arr=SortTestHelper::generateArray(n,0,n);
int *arr1=SortTestHelper::copyArray(arr,n);
int *arr3=SortTestHelper::copyArray(arr,n); 

SortTestHelper::testSort("QuickSort",QuickSort,arr,n);
SortTestHelper::testSort("QuickSort2",QuickSort2,arr1,n);
SortTestHelper::testSort("QuickSort3",QuickSort3,arr3,n);
cout<<"swaptimes:"<<count1<<" "<<count2<<" "<<count3<<endl;
cout<<endl;
SortTestHelper::testSort("NearlyOrderedQuickSort",QuickSort,arr2,n);
SortTestHelper::testSort("NearlyOrderedQuickSort2",QuickSort2,arr4,n);
SortTestHelper::testSort("NearlyOrderedQuickSort3",QuickSort3,arr6,n);
cout<<"swaptimes:"<<count1<<" "<<count2<<" "<<count3<<endl;

delete[] arr;
delete[] arr1;
delete[] arr2;
delete[] arr3;
delete[] arr4;
delete[] arr6;
return 0;

}

Answer 1

liuyubobobo 2019-01-26 02:27:12

在现代计算机上，测试出的算法的运行效率，不仅仅和逻辑有关，还和很多因素有关，如所使用的语言，所使用的编译器版本，编译器的优化方式，具体的实现方式，所运行的操作系统和当时的操作系统的状态。所以，通常，在现代计算机上，学习算法的过程，我们关注的是“趋势”，而不要（其实也无法）在毫秒级别的性能上做比较：）

所谓的趋势，就是真正体现我们的算法改进的地方，同时有着可以感知到的巨大性能差异的地方，比如：

选择排序稳定的比归并排序慢一大截；

对于近乎有序的数组，随机化后的快排稳定的远远快于没有随机化的快排；

对于包含大量重复元素的数组，二路快排和三路快排稳定快于一路快排；同时三路快排应该比二路快排快。

对于其他侧面的比较，只要没有巨大的差异，都可以忽略。比如对于你的数据，百万数据量，有0.05s（50ms）的差距，这个差距，在现代计算机上，很难叫差距。其实，对于算法的学习，我个人也根本不建议比较同复杂度算法之间的性能差异。这本身也不是我们学习算法的目的。我们学习算法的最首要的目的，是在复杂度上的超越。在看我上面举的例子：

选择排序稳定的比归并排序慢一大截：

因为选择排序是O(n^2)的，归并排序是O(nlogn)的；

对于近乎有序的数组，随机化后的快排稳定的远远快于没有随机化的快排：

因为对于近乎有序的数组，不随机化的快排将退化成O(n^2)的，随机以后快排的复杂度期望回到了O(nlogn)；

对于包含大量重复元素的数组，二路快排和三路快排稳定快于一路快排；同时三路快排应该比二路快排快:

因为对于包含大量重复元素的数组，一路快排退化成O(n^2)的，二路快排和三路快排则是O(nlogn)的：）

继续加油！：）

• 提问者 慕UI4716311 #1

  好的谢谢您