leetcode496 看到了单调栈解法的疑问

Question

老师，496题，我做法很传统，就如下图：拿着nums1中的每个数字到nums2中遍历，一旦找着了，那么就在nums2中这个找着的位置的下一个位置开始新的for循环，接着在此for循环中找比nums1此时遍历到的数字大的数字，如果有，就放在res[i]中，如果没有 res[i]=-1,这是我的方法，比较舒服，容易想。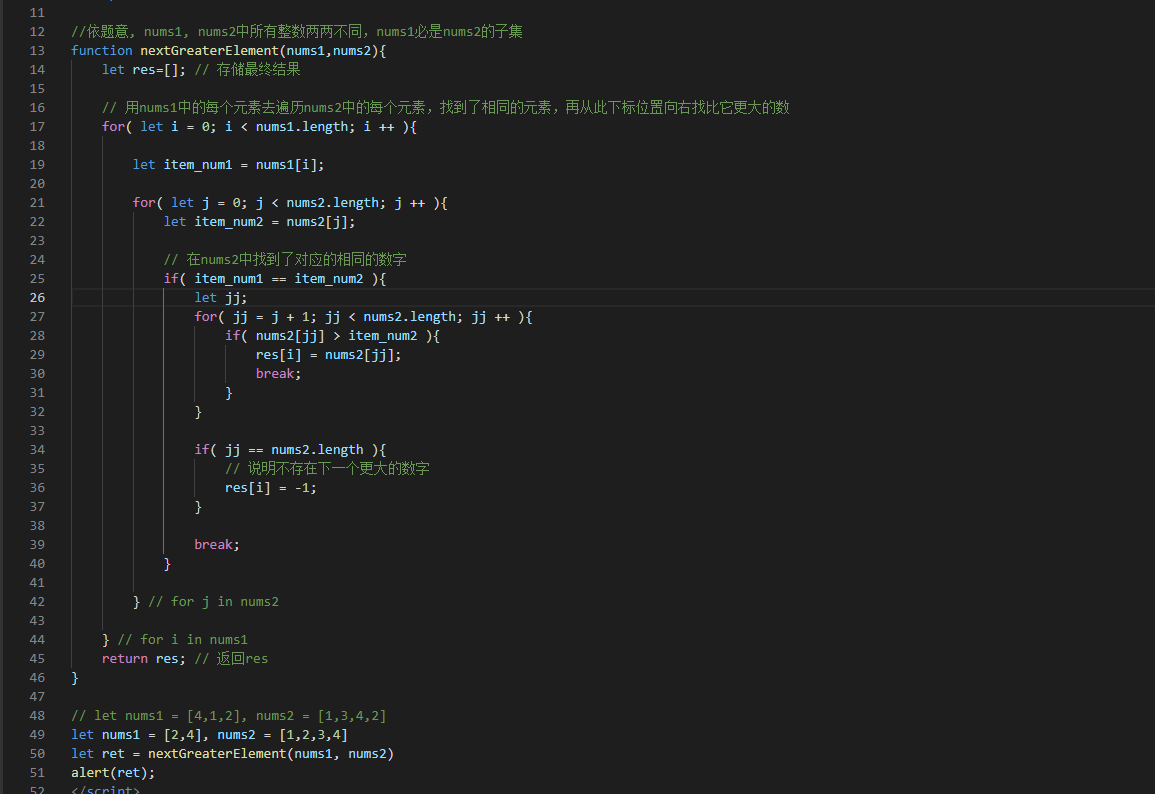

然后我看了您的496的解法，注释上写着 mono stack, 然后我就去网上查了下，发现是单调栈，哈哈哈，单调栈这个定义我能理解，但是和496题结合起来，以久leetcode 84(柱状矩形最大面积，这个我自己也会用普通多重循环的笨方法)，这些是单调栈的应用，不过我在网上琢磨了一两天，还是取不到他的精妙之处，没领会，老师，你能点一下吗，:)

Answer 1

liuyubobobo 2022-01-06 02:22:58

单调栈是我最害怕解释的一类问题，因为真的很难解释清楚，不是写一两段话就能解释清楚的。真要解释清楚，以我的风格，要搞一两节视频了。

对于单调栈，我强烈看这个题解（这个题解的作者也是我的课程的学生：）），写得非常清晰，配合了图示。现在有同学问我单调栈的问题，我近乎一率推荐看这个题解：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/bao-li-jie-fa-zhan-by-liweiwei1419/

理解了这个题解，你近乎一定能明白在 84 号问题下是如何使用单调栈求解的了。然后，记住：

单调栈的核心应用，就是在一个数组中，寻找：

1）**每个**元素右边第一个比这个元素大的元素（或位置）；

2）**每个**元素右边第一个比这个元素小的元素（或位置）；

3）**每个**元素左边第一个比这个元素大的元素（或位置）；

4）**每个**元素左边第一个比这个元素小的元素（或位置）；

见到这个应用，就可以上单调栈。暴力做是 O(n^2) 的，单调栈是 O(n) 的。

这也就是为什么 496 虽然是一个 easy 问题，直接暴力就可以通过。但一旦你知道（并且熟悉）单调栈，就会更倾向于直接用单调栈。因为是太明显的单调栈问题。（但如果不知道单调栈，肯定想不到。）

==========

另外，单调栈是在面试中近乎一定不会遇到的问题。属于竞赛级别的技巧。因为它的应用实现不够广泛，思维虽然巧妙，但也不是一个特别通用的，普遍的，可泛化的思维方式。虽然有同学告诉我在面试中碰到单调栈的问题，但是，或者：

1）有别的解法，可以绕过单调栈；

2）或者是力扣的原题（虽然这样很无聊）；

3）我坚信有没有是用单调栈做出这个问题，也不是面试成功与否的关键标志；

继续加油！：）

• 提问者 甲骨文_0001 #1

  谢谢🙏

• 提问者 甲骨文_0001 #2

  老师，我看了你的leetcode 84题，有线段树的解法，线段树本身的概念能明白，然后这道题目结合线段树的思路我没看明白，可以解释一下吗，谢谢哈🙏

• liuyubobobo 回复 提问者 甲骨文_0001 #3

  假设 H[l, r] 区间的最小高度是 H[min_index]。则在这个区间的最大的矩形，或者就是 H[min_index] * (r - l + 1)（即整个区间的宽度乘以这个最小高度），或者是 H[l, min_index - 1] 区间里的最大矩形，或者是 H[min_index + 1, r] 里的最大矩形（这两个区间里的最大矩形都肯定不会用上 H[min_index] 了，应该很好理解。）递归即可。
  
  线段树用于快速（logn 的时间）找到 [l, r] 区间里的最小值。
  
  继续加油！：）

点开查看后面1条评论