Leetcode 2569 线段树区间更新

Question

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @param {number[][]} queries
 * @return {number[]}
 */
var handleQuery = function(nums1, nums2, queries) {
    let tree = new SegTree(nums1)
    let sum = nums2.reduce((tmp, cur)=>tmp+cur) // nums2求和

    let list = []

    for( let i = 0; i < queries.length; i ++ ){
        // 操作类型1 对 nums1数组进行更新
        if( queries[i][0] == 1 ){
            let left = queries[i][1], right = queries[i][2];
            // 从下标left,到 right依次对tree作单个值更新
            for( let j = left; j <= right; j ++ ){
                tree.set(j, 1 - nums1[j] /* 翻转: 1=>0, 0=>1 */)
            } // for j

        }else if( queries[i][0] == 2 ){
            // 操作类型 2
            sum += tree.query(0, nums1.length - 1) * queries[i][1];
        }else if( queries[i][0] == 3 ){
            // 操作类型3
            list.push(sum);
        }

    } // for i queries

    return list;
};

// 线段树
class SegTree{
    constructor(nums) {
         const N = nums.length;
         this.N = N;
       //  this.data = [...nums]
       // ******* 这里nums数组给到this.data，两者指向同一块空间 *********
         this.data = nums;
         this.tree = Array(4 * N).fill(0);
         this.build(0, 0, N - 1, nums)
    }

    build(treeIndex, left, right, nums) {
        if( left == right ){
            this.tree[treeIndex] = nums[left]
            return
        }

        let leftTreeIndex = 2 * treeIndex + 1
        let rightTreeIndex = 2 * treeIndex + 2

        let mid = Math.floor( (left + right) / 2 )
        this.build(leftTreeIndex, left, mid, nums)
        this.build(rightTreeIndex, mid+1, right, nums)

        this.tree[treeIndex] = this.tree[leftTreeIndex] + this.tree[rightTreeIndex]
    }

    // 查询
    query( queryL, queryR ){
        return this._query(0, 0, this.N - 1, queryL, queryR)
    }

    _query( treeIndex, left, right, queryL, queryR ){
        if( left == queryL && right == queryR ){
            return this.tree[treeIndex]
        }
        let mid = Math.floor( (left + right) / 2 )
        let leftTreeIndex = 2 * treeIndex + 1
        let rightTreeIndex = 2 * treeIndex + 2

        if( queryL >= mid + 1 ){
            return this._query(rightTreeIndex, mid + 1, right, queryL, queryR)
        }else if( queryR <= mid ){
            return this._query(leftTreeIndex, left, mid, queryL, queryR)
        }

        let leftResult = this._query(leftTreeIndex, left, mid, queryL, mid)
        let rightResult = this._query(rightTreeIndex, mid + 1, right, mid + 1, queryR)
        return leftResult + rightResult
    }

    // 单个更新, 更新原数组index处值为e
    set( index, e ){
        this.data[index] = e
        this._set(0, 0, this.N - 1, index, e)
    }

    // 在以treeIndex为根的线段树中更新index的值为e
    _set( treeIndex, left, right, index, e ){
        if( left == right ){
            this.tree[treeIndex] = e;
            return
        }

        let mid = Math.floor( (left + right) / 2 )
        let leftTreeIndex = 2 * treeIndex + 1
        let rightTreeIndex = 2 * treeIndex + 2

        if( index >= mid + 1 ){
            this._set(rightTreeIndex, mid+1, right, index, e)
        }else{
            this._set(leftTreeIndex, left, mid, index, e)
        }

        this.tree[treeIndex] = this.tree[leftTreeIndex] + this.tree[rightTreeIndex]
    }
}

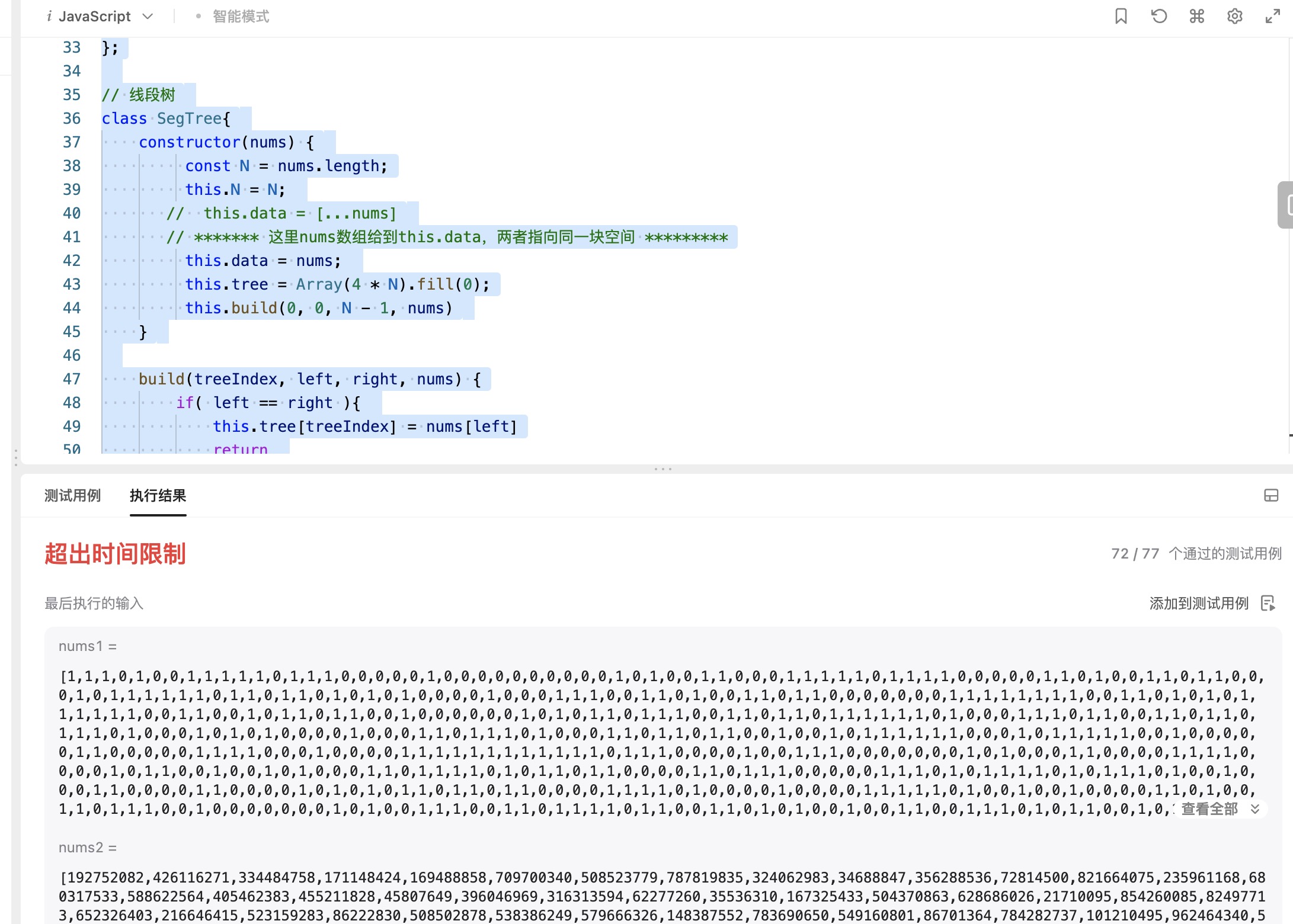
老师,线段树这个结构我能懂，然后我们课上讲的是对树上进行单个值更新，也很好懂， 这道题目是昨天的每日一题，我就想巩固一下线段树的知识，然后自己也写了一下，这题是区间更新，但是我自己是通过单个值set更新区间【left, right】。 倒在了54号用例上，调试了三四个钟头，我没调试出来，需要老师帮忙看看哈，另外我看题解里面还讲了lazy更新，能否也帮我点拨下: )

Answer 1

liuyubobobo 2023-07-28 12:09:52

线段树的懒更新不是一句话两句话能解释清楚的，我只能推荐一些资料。

我见过的关于懒更新写得最好的（入门级）的资料是这个：https://leetcode.com/articles/a-recursive-approach-to-segment-trees-range-sum-queries-lazy-propagation/

这份资料搞明白了自己手写懒更新应该就没问题了。

更多进阶资料推荐这里，页面内搜索“Segment Tree”下面的所有文章：https://codeforces.com/catalog

另外，懒更新在面试中 200% 不可能出现。

继续加油！：）

• 提问者 甲骨文_0001 #1

  嗯嗯，我订正了一版，现在只有线段树单个值更新的作法，超过时间限制了，上述材料中我好好消化一下，虽然面试不会考，但是作为工程师，还是有必要尽量拓展一下思路，我会再写一版，再给老师您看看哈。。。