逻辑回归二分类问题

Question

老师，帮我纠正一下思路，我不太理解图片上的问题，不知道为什么图1中的y’=Θx=0时是图2中的t=0对应概率p的分界点。不知道他们两者是怎么联系一起的，是不是因为图1我画的不对进而理解错了。我把值y’=Θx理解成一个样本的值了，但是样本值的y肯定是没有所谓的等于0的特殊性意义的。

Answer 1

liuyubobobo 2019-08-04 14:47:28

我不确定我是不是正确的的理解了你的问题。

首先，整个逻辑刚回归的逻辑是这样的。逻辑回归认为，对于一个样本x来说，他能分成a类或者b类的概率，和这个样本的特征相关。所以，靠θx的值，能够计算出，x是a的概率。（相应的，也就知道了x不是a的概率，也就是x是b的概率。）

所以，我们是用θx拟合一个概率值。因此，你的图1是错误的。你的图一是一个分类问题的示意图，但逻辑回归是让θx拟合一个概率值，这是它叫逻辑回归的原因。他是一个回归问题。所以，应该这样一个示意图（横轴是特征，纵轴是概率p）：

但是，因为我们不能保证 θx 在[0,1]之间，而θx是在拟合概率值，概率一定在[0,1]之间，所以，我们在θx外面添加一个sigmoid函数，这样，就保证了sigmoid(θx)在[0, 1]之间，

相当于，我们建立的关系是：p = sigmoid(θx)，表示x是某一类的概率。那么 1 - p 就是x是另一类的概率。

在这个基础上，我们又知道每一个x对应的实际y（是0还是1），我们就有了这一小节的推导，定义出了损失函数。

请基于这些文字的内容，再回顾一下这一章的第一小节，理解一下这个过程：）

继续加油！：）

• 提问者 霸气的小羊 #1

  谢谢老师，其实就是不理解，为什么θx为正时，数据是偏好取1的，为负时数据是偏好取0的。Decision_function的数据为什么就能体现到样本集的二分类上。第一节课说到将θx看做一个特征，根据公式p=σ(t)可以去拟合一个概率,从数学的角度确实可以理解，但是不理解的是Decision_function得到的数据中取值为0的时候为什么刚好就是两种样本的分类边界了，而且刚好一个样本种类对应的数据在负值，另一个样本种类对应的数据在正值，感觉太神奇了。是不是因为这个问题用图形话的思维模式去思考的时候太过复杂了，还是我理解的偏差比较大。

• liuyubobobo 回复 提问者 霸气的小羊 #2

  为什么θx为正时，数据是偏好取1的，为负时数据是偏好取0的？这是我们的定义，反过来定义没问题的。但是损失函数要根据这个定义变化。仔细体会一下，我们的损失函数的推导中，是隐含这一定义的。至于你说的“Decision_function得到的数据中取值为0的时候为什么刚好就是两种样本的分类边界”，这就是我们选取sigmoid函数的原因。sigmoid函数的性质保证了θx > 0，则p的估计值大于0.5；θx < 0，则p的估计值小于0.5，而 θx = 0，则p的估计值等于0.5，即分两类概率各为50%，也就是决策边界：）

• 提问者 霸气的小羊 回复 liuyubobobo #3

  谢谢老师，我在体会一下。

点开查看后面1条评论

Answer 2

提问者 霸气的小羊 2019-08-07 22:43:35

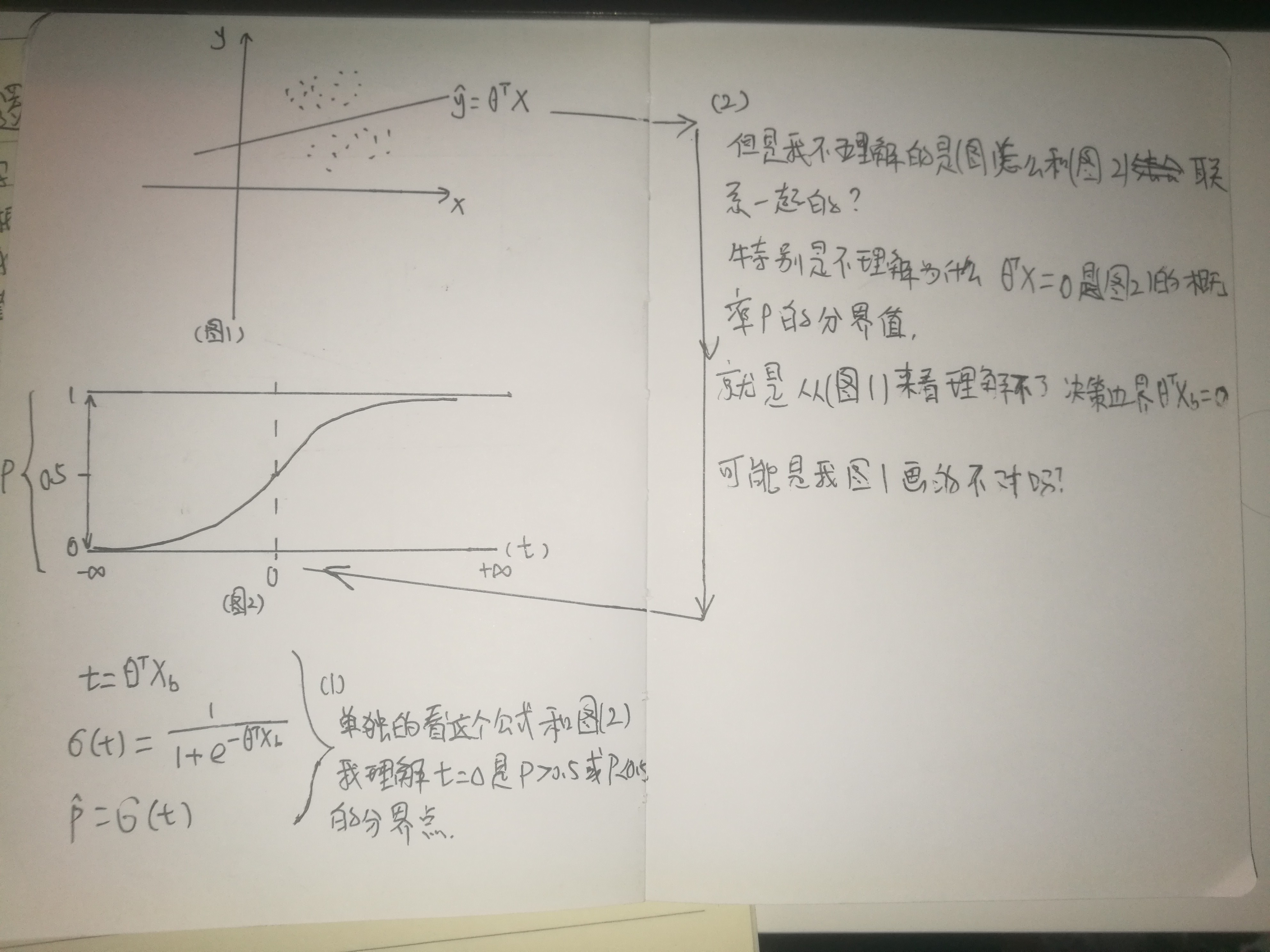
这个问题的思考有了进一步的进展，我梳理下，

其实从数学公式的角度来看，设定y'=ΘX，p=1/1+e^t，t=ΘX确实很好的满足了当前数据集的一些性质，可以想象成是为了解决逻辑回归问题才引入的这样几个公式，而这几个公式恰好符合当前二分类数据的性质，特别是要求y'=t做为假设的前提,才使得概率p和y'有了一定的对照关系，因为0<p<1,所以t要满足-∞<t<+∞。反过来也是一样的，因为t满足-∞<t<+∞，所以p满足0<p<1。其实概率p和预测值t之间相互因果的关系，抛开其他不谈，仅从公式就可以发现。就好比是因为a所以求得b，反过来因为b所以求得a，当a和b相互都需要彼此为自己证明的时候，其实是谁也不能为谁证明的，问题将会变的很严重，因此当前ab有因果的前提是先预设了y'=t，y'=t我认为很重要，要问为什么重要，还是因为样本数据的性质决定了很重要，这也是我一开始很郁闷的地方,因为要使y'=t就要使得ΘX满足在从正到负都有值而且还必须有0值，但是一开始假如从线性回归拟合样本集的角度去理解y'=ΘX的时候，我们又对样本数据的性质没有很好的理解的话，怎么保证ΘX在-∞到+∞之间一定都有值，我们通过下降法最终求得的函数y'=ΘX就一定满足同时有正、有负、有0吗？就比如预测波士顿房价的时候函数ΘX可能是没有负值的，如果预测一个样本都是一些差的特征而房屋面积和房间数等重要特征都设定为0时不知道会不会有可能使房价为负的情况，如果没有，那么总有一些别行业的数据集通过样本特征拟合的曲线函数是在x轴上方的，但是这个问题放在二分类的数据集上问题就变的确定了。

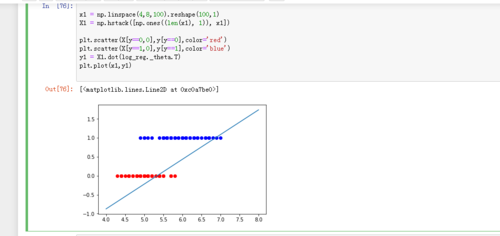
上面的图做一下阐述：x轴是鸢尾花样本的一个特征，y轴是鸢尾花样本标签，此时标签结果只有0和1两种分类。这条斜线是4-8之间100个特征点对应的分类结果y'，首先，为什么y'不是0或者1，而是所有实数解。这是因为此时求得的函数值y'还没有当做t带入概率p的公式，因为此时的y'=ΘX是通过梯度下降法最小化损失函数J(Θ)求得的，还要特别说明的是：如下图所示，我们需要通过梯度下降法求得p使得损失函数J(Θ)最小，同样可以说是求Θ使得损失函数J(Θ)最小，因为p=1/1+e^t ，我们同样可以说求t，此时t=y，也就是求y使得损失函数J(Θ)最小。

所以我们此时求得的y是-∞到+∞之间的数，而不是0或者1，但是可以通过p=1/1+e^t ，进一步求得p的值。

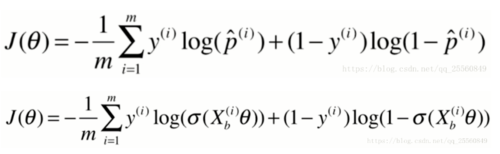
那么为什么我们求得的y'=ΘX函数一定是斜线，而不是与x轴平行呢，因为如果我们求的y=ΘX与x轴平行的话就终于可以推翻了我们一开始的假设y'=t。因为我们求的是损失函数J(Θ)的极小值，说明此时的拟合效果还是很好的，假如此时y=ΘX与x轴平行,y取常数1，此时p<0.5,也就是说所有的测试样本x_test的值将只有一种分类结果，同样假设y取-5，此时p>0.5,会发现概率p不受样本x_test值的影响，此时的损失函数J(Θ)将不是最小值，变的非常大，所以说y'=ΘX函数一定不与x轴平行，也就是明说了在逻辑回归中ΘX在一定有正值、有负值、有0值。

（其实一开始为什么t=ΘX？是因为假设ΘX有正有负有0 (t=2ΘX或3ΘX应该也是不影响的)，但是为什么ΘX有正有负有0？是因为我们假设t=ΘX已经相等了然后根据梯度下降法求得的Θx确实有正有负有0，好吧，有绕进去了。可能唯一不变的大前提还是因为样本数据是二分类问题所以决定了这样做可以）。

所以总结一下，就是样本数据集的性质决定了函数的性质，在茫茫大海中找到的p和t就好比是螺丝和螺帽，刚好可以解决当先的算法问题。

• liuyubobobo #1

  大赞思考！感谢你的分享：）

• 提问者 霸气的小羊 回复 liuyubobobo #2

  水平有限，我就只能思考到这个程度了，感觉原因和结果之间是在一个内部系统里面相互纠缠相互影响的，可能这类问题有专门的学术研究。