老师问一个迪杰斯特拉最短路径算法的问题
图是这么个图，出发点为G（中心）。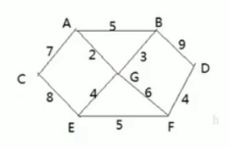
经过循环之后，只输出了第一轮结果，也就是：
A(2) B(3) N N E(4) F(6) G(0) 。
然后我通过众多测试也发现了问题所在，就是在循环中只进行了第一次循环。
我的问题是：如何以当前距离最小的节点为起点，继续遍历后面的点？
（前面为了希望能帮老师节约一些时间，所以就写了简略版，后面有完整的代码）
其中的一些数据是：
public int[] already;//顶点集合：记录各个顶点是否访问过，动态更新
public int[] previsited;//前驱顶点集合：记录当前节点的前一个顶点下标
public int[] dis;//距离集合，记录了出发顶点到其他所有顶点的距离
private char[] vertex;//顶点
private int[][] matrix;//邻接矩阵
private visitedvertex0 vv;//在图中定义已经访问的集合
public void dijkstra1(int index) {
vv = new visitedvertex0(vertex.length, index);//1. 构造器中完成初始化
//初始化第一个节点
for(int i = 0 ; i < matrix[index].length ; i ++) {
vv.dis[i] = matrix[index][i];
}
vv.dis[index] = 0;
while(vv.already != null) {// 2. 循环
// 3.获取距离最小，并置访问
int v0 = vv.getv0();
System.out.println("this v0 =" +v0);
if (v0 != -1)
{
vv.already[v0] = 1;
// 4.遍历v0节点，找到未访问节点
for (int j = 0; j < matrix[v0].length; j++) {
if (vv.already[j] != 0) {
// 5.判断距离并更新
int thisdistance = matrix[v0][j];// 获取v0-j的这条边
if (thisdistance + vv.dis[v0] < vv.dis[j]) {//更新距离
vv.dis[j] = thisdistance + vv.dis[v0];
vv.previsited[j] = v0;
}
}
}
System.out.println("success");
}
else break;
//问题：这只进行了第一次循环，找出了第一次的最短路径。如何以当前距离最小的节点为起点继续寻找？
}
}
//获取未访问过最小节点的下标。在我的java代码里面这两个方法不是放在同一个类里面的
public int getv0() {
int min = 65535;
int index = -1;
int[] isvisited = new int[already.length];
//遍历所有节点
for(int i = 0 ; i < already.length ; i++) {
//获取未访问过最小节点的下标
if(already[i] == 0 && dis[i] < min) {
index = i;
min = dis[i];
}
isvisited[i] = 1;
System.out.println("最小值"+min+"最小节点下标"+index);
}
return index;
}
完整代码如下：
package Chapter5;
import java.util.Arrays;
public class Mydijkstra {
public static void main(String[] args) {
char[] vertex = {'A','B','C','D','E','F','G'};
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;
matrix[0] = new int[] {N,5,7,N,N,N,2};
matrix[1] = new int[] {5,N,N,9,N,N,3};
matrix[2] = new int[] {7,N,N,N,8,N,N};
matrix[3] = new int[] {N,9,N,N,N,4,N};
matrix[4] = new int[] {N,N,8,N,N,5,4};
matrix[5] = new int[] {N,N,N,4,5,N,6};
matrix[6] = new int[] {2,3,N,N,4,6,N};
//创建Graph
Graph0 g = new Graph0(vertex,matrix);
/*
g.show();
g.Dijkstra(6);
g.resultshow();
*/
System.out.println("=====================");
g.dijkstra1(6);
g.resultshow();
}
}
class Graph0{
private char[] vertex;//顶点
private int[][] matrix;//邻接矩阵
private visitedvertex0 vv;//在图中定义已经访问的集合
public Graph0(char[] vertex,int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
public void show() {
for(int [] a : matrix) {
System.out.println(Arrays.toString(a));
}
}
public void dijkstra1(int index) {
vv = new visitedvertex0(vertex.length, index);//1. 构造器中完成初始化
//初始化第一个节点
for(int i = 0 ; i < matrix[index].length ; i ++) {
vv.dis[i] = matrix[index][i];
}
vv.dis[index] = 0;
while(vv.already != null) {// 2. 循环
// 3.获取距离最小，并置访问
int v0 = vv.getv0();
System.out.println("this v0 =" +v0);
if (v0 != -1)
{
vv.already[v0] = 1;
// 4.遍历v0节点，找到未访问节点
for (int j = 0; j < matrix[v0].length; j++) {
if (vv.already[j] != 0) {
// 5.判断距离并更新
int thisdistance = matrix[v0][j];// 获取v0-j的这条边
if (thisdistance + vv.dis[v0] < vv.dis[j]) {//更新距离
vv.dis[j] = thisdistance + vv.dis[v0];
vv.previsited[j] = v0;
}
}
}
System.out.println("success");
}
else break;
//问题：这只进行了第一次循环，找出了第一次的最短路径。如何以当前距离最小的节点为起点继续寻找？
}
}
public void resultshow() {
vv.finalshow();
}
}
class visitedvertex0{
public int[] already;//顶点集合：记录各个顶点是否访问过，动态更新
public int[] previsited;//前驱顶点集合：记录当前节点的前一个顶点下标
public int[] dis;//距离集合，记录了出发顶点到其他所有顶点的距离
//传入的是节点总数、出发顶点对应下标。并且初始化
public visitedvertex0(int length,int index) {
this.already = new int [length];//除了自己置1外，其他置空
this.already[index] = 1;
this.previsited = new int[length];//初始置0
this.dis = new int[length];
//初始化dis数组，除了自己外设置为最大
for(int i = 0 ; i < dis.length ; i ++) {
dis[i] = 65535;
}
dis[index] = 0;
}
//判断index顶点是否被访问过
public boolean isvisited(int index) {
return already[index] == 1;
}
//更新index顶点的前驱为prev节点
public void updatepre(int index,int prev) {
previsited[index] = prev;
}
//获取出发顶点到index顶点的距离
public int getDis(int index) {
return dis[index];
}
//获取未访问过最小节点的下标
public int getv0() {
int min = 65535;
int index = -1;
int[] isvisited = new int[already.length];
//遍历所有节点
for(int i = 0 ; i < already.length ; i++) {
//获取未访问过最小节点的下标
if(already[i] == 0 && dis[i] < min) {
index = i;
min = dis[i];
}
isvisited[i] = 1;
System.out.println("最小值"+min+"最小节点下标"+index);
}
return index;
}
//输出三个数组的结果
public void finalshow() {
System.out.println("==========");
for(int i : already) {
System.out.print( i + " , ");
}
System.out.println();
for(int i : previsited) {
System.out.print( i + " , ");
}
System.out.println();
for(int i : dis) {
System.out.print( i + " , ");
}
System.out.println();
System.out.println("最短路径：");
//直接输出最短距离
char[] vertex = {'A','B','C','D','E','F','G'};
int count = 0 ;
for(int i : dis) {
if(i != 65535) {
System.out.print(vertex[count] +"(" + i + ") ");
}
else {
System.out.print(" N ");
}
count++;
}
System.out.println();
}
}
705
收起
正在回答 回答被采纳积分+3
1回答
liuyubobobo
2019-08-25 17:41:31
-
是的，可以参考我的公号文章：https://mp.weixin.qq.com/s?__biz=MzU4NTIxODYwMQ==&mid=2247484417&idx=1&sn=f774306b0ea726d979eba0c13b75496f&chksm=fd8cab47cafb2251f7bebcc3c540d0216989499ed9ad0cf0f3bd8817412ea79ea6b31cc66a8d&token=71131388&lang=zh_CN#rd 加油！
有任何疑惑可以回复我~ 2019-08-25 18:12:11
